Symmetrie von Funktionen
Das Zeichnen der Graphen von Funktionen lässt sich durch das Vorhandensein von Symmetrie(n) stark vereinfachen.
Insbesondere treten bei den Graphen zwei Grundsymmetrien auf:
- Achsensymmetrie (Axialsymmetrie)
- Punktsymmetrie (Zentralsymmetrie)
Mit Blick auf einige spezielle Funktionen (vor allem periodische Funktionen), z.B. die Tangensfunktion , ist auch eine so genannte Verschiebungssymmetrie (Axialverschiebung) von Interesse.
Achsen- und Punktsymmetrie
Die Bedingungen für axialsymmetrische und zentralsymmetrische Graphen sind in der Abbildung angegeben. Die entsprechenden Funktionen werden gerade bzw. ungerade Funktionen genannt.
-
Gerade und ungerade Funktionen
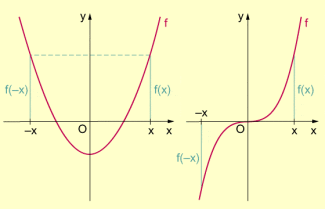
- Eine Funktion f mit dem Definitionsbereich heißt gerade Funktion genau dann, wenn mit auch ist und wenn gilt:
für alle - Eine Funktion f mit dem Definitionsbereich heißt ungerade Funktion genau dann, wenn mit auch ist und wenn gilt:
für alle
Bei ganzrationalen Funktionen kann man eine vorhandene Symmetrie relativ einfach erkennen.
Treten im Funktionsterm nur gerade Potenzen von x auf, ist also mit , so gilt stets . Treten andererseits nur ungerade Potenzen von x auf, ist also mit , so gilt stets .
Für ganzrationale Funktionen f mit mit lässt sich somit allgemein formulieren:
- Die Funktion f ist genau dann gerade, wenn im Funktionsterm nur Potenzen von x mit geraden Exponenten auftreten.
Anmerkung: Wegen gilt auch als Summand mit geradem Exponenten von x. - Die Funktion f ist genau dann ungerade, wenn im Funktionsterm nur Potenzen von x mit ungeraden Exponenten auftreten.
Beispiel 1: Die Funktionen , und sind auf Symmetrie zu untersuchen.
Der Graph von f ist achsensymmetrisch zur y-Achse, da alle Potenzen von x gerade sind; der Graph von g ist punktsymmetrisch zum Koordinatenursprung, da alle Potenzen von x ungerade sind. Demzufolge ist f eine gerade und g eine ungerade Funktion.
Die Funktion h ist weder gerade noch ungerade.
Beispiel 2: Die Funktionen f mit und g mit sind auf Symmetrie zu untersuchen.
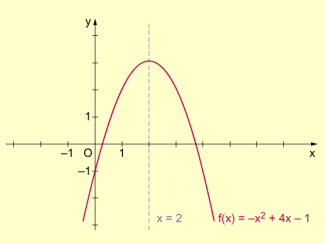
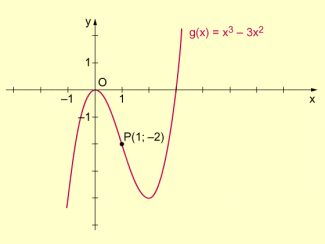
Nach den oben herangezogenen Kriterium sind f und g weder gerade noch ungerade. Trotzdem weisen ihre Graphen (s. Bilder 2 und 3) eine Symmetrie auf.
Der Graph von f ist achsensymmetrisch zur Geraden , der Graph von g zentralsymmetrisch zum Punkt .
Beispiel 3: Es ist zu untersuchen, ob die Funktion f mit gerade oder ungerade ist.
Man bildet und erhält:
.
Die Funktion f ist also ungerade.
Beispiel 4: Es sind Symmetrie und Monotonieverhalten der quadratischen Funktion sind zu bestimmen.
Die Scheitelpunktsform lautet , d.h., der Scheitelpunkt hat die Koordinaten . Das bedeutet, der Graph der Funktion ist symmetrisch zur Geraden . Durch den Scheitelpunkt S ist das Monotonieverhalten der nach oben geöffneten Parabel bestimmt. Die Funktion f ist im Intervall streng monoton fallend und im Intervall streng monoton wachsend.
-
Beispiel eines achsensymmetrischen Funktionsgraphen
-
Beispiel eines punktsymmetrischen Funktionsgraphen
Suche nach passenden Schlagwörtern
- Achsensymmetrie
- ungerade
- zentralsymmetrisch
- periodisch
- gerade
- Punktymmetrie
- axialsymmetrisch
- Monotonie
- Stauchung
- verschiebungssymmetrisch
- ganzrationale Funktionen
- Funktionen
- achsensymmetrisch
- Axialverschiebung
- Streckung
- Zentralsymmetrie
- Symmetrie
- Axialsymmetrie
- Graphen
- Kosinusfunktion
- punktsymmetrisch

