Nullstellen linearer und quadratischer Funktionen

Allgemein versteht man unter einer Nullstelle einer Funktion $f$ diejenige Zahl $x_0\in D_f$, für die $f\left(x_0\right)=0$ gilt. Nullstellen zu berechnen heißt demnach, alle Lösungen der Gleichung $f\left(x\right)=0$ zu ermitteln. Näherungsweise kann man Nullstellen auch grafisch bestimmen. Man zeichnet den Graphen und beim Schnittpunkt des Graphen mit der $x$-Achse liest man den Abszissenwert als Nullstelle ab.
Anmerkung: Nicht der Schnittpunkt des Graphen mit der $x$-Achse wird als Nullstelle angesehen, sondern nur die $x$-Koordinate dieses Punktes.

Nullstellen linearer Funktionen

Lineare Funktionen sind allgemein von der Form $f\left(x\right)=mx+n(\text{mit}m,n\in ℝ)$ und stellen ganzrationale Funktionen 1. Grades dar. Funktionen 1. Grades haben immer nur eine Nullstelle, nämlich die Lösung der linearen Gleichung $0=mx+n$.

• Beispiel 1: Man bestimme die Nullstelle von $\text{f(x)}=\frac{\text{2}}{\text{3}}\text{x}-\text{1}$.

Zur Berechnung der Nullstelle setzt man für $\text{f(x)}$ den Wert Null ein und löst die Gleichung:
$0=\frac{2}{3}x-1\Rightarrow x=\frac{3}{2}$
Auf grafischem Weg kann man mithilfe des Anstiegs $m=\frac{2}{3}$ und des Abschnittes auf der $y$-Achse $n=1$ den Graph sofort zeichnen und liest als Schnittpunkt von Graph und $x$-Achse den Wert $x\approx \mathrm{1,5}$ ab.

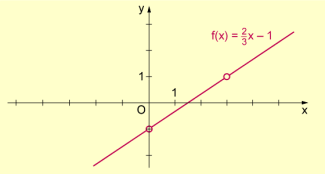
Allgemein gilt: Ist eine lineare Funktion in der Form $f\left(x\right)=mx+n(\text{mit}m,n\in ℝ;m\ne 0)$ gegeben, dann berechnet man deren Nullstelle $x_0$ nach $x_0=-\frac{n}{m}$.

Nullstellen quadratischer Funktionen

Die allgemeine Form quadratischer Funktionen als ganzrationale Funktionen 2. Grades ist $f\left(x\right)=a{x}^2+bx+c$. Zum Bestimmen der Nullstellen erhält man Gleichungen der Form $a{x}^2+bx+c=0$ mit den Lösungen ${\text{x}}_{\text{1;}\text{2}}=-\frac{\text{b}}{\text{2a}}\pm \sqrt{\frac{{\text{b}}^{\text{2}}-\text{4a}\cdot \text{c}}{{\text{4a}}^{\text{2}}}}.$

Eine quadratische Funktion hat maximal zwei Nullstellen.

• Beispiel 2: Von den folgenden quadratischen Funktionen sind die Nullstellen zu ermitteln:
  $\begin{array}{l}a)f\left(x\right)=x^2-6x+8\\ b)g\left(x\right)=x^2-3x+\mathrm{2,25}\\ c)h\left(x\right)={\left(x+3\right)}^2+2\end{array}$

Lösung der Teilaufgabe a):
$\begin{array}{l}{\text{x}}_{\text{1;}\text{2}}=\text{3}\pm \sqrt{\text{9}-\text{8}}\\ x_1=4x_2=2\end{array}$
Die Funktion $f$ hat zwei Nullstellen.

Lösung der Teilaufgabe b):
$\begin{array}{l}{\text{x}}_{\text{1;}\text{2}}=\frac{\text{3}}{\text{2}}\pm \sqrt{\frac{\text{9}-\text{9}}{\text{4}}}\\ x_1=\mathrm{1,5}\end{array}$
Die Funktion $g$ hat genau eine Nullstelle.

Lösung der Teilaufgabe c):
Man liest unmittelbar die Koordinaten des Scheitelpunktes $S\left(-3;2\right)$ ab, das ist ein Punkt oberhalb der $x$-Achse, und wegen der Öffnung der Parabel nach oben gibt es keine Nullstelle.

Sind zwei Nullstellen $x_1$ und $x_2$ vorhanden, dann gilt nach dem Satz von VIETA:
$x_1+x_2=-\frac{b}{a}$ und $x_1\cdot x_2=\frac{\text{c}}{\text{a}}$

Hieraus folgt für $f\left(x\right)$:
$\begin{array}{l}f\left(x\right)=a{x}^2+bx+c=a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)\\ =a\left(x^2+x\left(-x_1-x_2\right)+x_1\cdot x_2\right)\\ =a\left(x^2-{xx}_1\cdot -x\cdot x_2+x_1\cdot x_2\right)\\ =a\left(x-x_1\right)\cdot \left(x-x_2\right)\text{für}a\ne 0\end{array}$

Auf diese Weise kann man den Funktionsterm einer quadratischen Funktion als Produkt von Linearfaktoren schreiben.
Sind andererseits die Nullstellen $x_1$ und $x_2$ einer ansonsten unbekannten quadratischen Funktion gegeben, dann ist ihr Funktionsterm auf jeden Fall vom Typ $f\left(x\right)=a\left(x-x_1\right)\cdot \left(x-x_2\right)$.

• Beispiel 3: Gegeben sind die Nullstellen $x_1=3$ und $x_2=-5$ einer quadratischen Funktion $f$.
  Man bestimme eine Funktionsgleichung für $f$.

In $f\left(x\right)=a\left(x-x_1\right)\cdot \left(x-x_2\right)$ werden für $x_1$ und $x_2$ die gegebenen Werte eingesetzt, und man erhält
$\begin{array}{l}f\left(x\right)=a(x-3)\cdot (x+5)\\ f\left(x\right)=a(x^2+2x-15)\end{array}$

Damit ist der Funktionsterm von $f$ bis auf den Koeffizienten $a$ bestimmt. Für jeden Wert $a\in ℝ$ ergibt sich eine bestimmte Funktionsgleichung, z.B. $a=2$ liefert $f\left(x\right)=2x^2+4x-3$.