Nullstellen gebrochenrationaler Funktionen
Nullstellen einer gebrochenrationalen Funktion sind alle Nullstellen der ganzrationalen Zählerfunktion, die nicht gleichzeitig Nullstellen der Nennerfunktion sind. Damit ist das Bestimmen der Nullstellen gebrochenrationaler Funktionen auf die Nullstellenermittlung ganzrationaler Funktionen zurückgeführt.
Allgemein versteht man unter einer Nullstelle einer Funktion diejenige Zahl , für die gilt.
Ist bei einer gebrochenrationalen an einer Stelle die Zählerfunktion gleich null, d.h. gilt , so ist eine Nullstelle von , wenn gleichzeitig gilt.
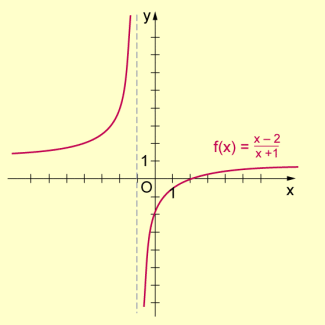
- Beispiel 1: Gegeben sei die Funktion mit (Definitionslücke). Es sind die Nullstellen zu bestimmen.
Zur Ermittlung der Nullstellen von setzt man die Zählerfunktion gleich null und löst die entstehende Gleichung, also:
Da für die Nennerfunktion , ist Nullstelle von .
-
Graph der Funktion des Beispiels 1
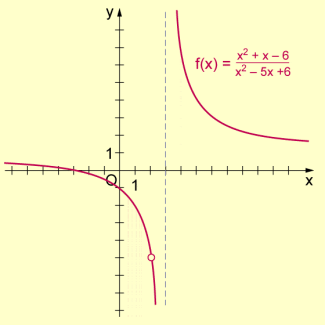
- Beispiel 2: Von der Funktion sind der Definitionsbereich und die Nullstellen zu bestimmen.
Die Funktion hat an den Stellen und Definitionslücken, da die Nennerfunktion für diese Werte gleich null ist.
Damit ist der Definitionsbereich .
Zur Berechnung der Nullstellen setzt man die Zählerfunktion gleich null und löst die folgende Gleichung:
Diese hat die Lösungen und .
An der Stelle liegt eine Nullstelle vor, da .
Da die Funktion für nicht definiert ist, existiert dort auch keine Nullstelle. Das bestätigt auch die grafische Darstellung der Funktion:
-
Graph der Funktion des Beispiels 2
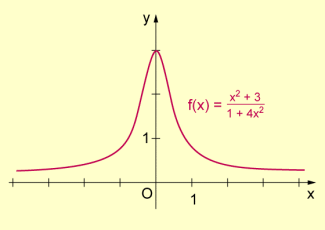
- Beispiel 3: Die Funktion ist auf Nullstellen zu untersuchen.
Die Funktion ist für alle definiert. Nullsetzen des Zählers führt auf die Gleichung , die im Bereich der reellen Zahlen keine Lösungen besitzt. Die Funktion hat folglich keine Nullstellen.
-
Graph der Funktion des Beispiels 3
Zusammenfassung
Nullstellen einer gebrochenrationalen Funktion sind alle Nullstellen der ganzrationalen Zählerfunktion, die nicht gleichzeitig Nullstellen der Nennerfunktion sind. Damit ist das Bestimmen der Nullstellen gebrochenrationaler Funktionen auf die Nullstellenermittlung ganzrationaler Funktionen zurückgeführt.

