Nullstellen von Wurzelfunktionen sowie Exponential- und Logarithmusfunktionen

Zur Klasse der nichtrationalen Funktionen gehören neben den trigonometrischen Funktionen die Wurzelfunktionen, die Exponential- und Logarithmusfunktionen. Zur Bestimmung der Nullstellen jener Funktionen untersucht man, an welchen Stellen $f\left(x\right)=0$ gilt. Im Folgenden wird dies exemplarisch an ausgewählten Funktionen demonstriert.

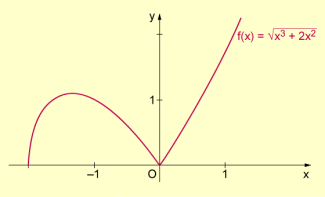
• Beispiel 1: Für die Funktion $f(x)=\sqrt{x^3+2x^2}$ sind der Definitionsbereich und die Nullstellen zu bestimmen.

Da die Wurzel nur aus nichtnegativen Zahlen gezogen werden kann, muss für den Radikanden gelten:
$x^3+2x^2\ge 0$ bzw. $x^2\left(x+2\right)\ge 0$
Da $x^2\ge 0$ für alle $x\in ℝ$ gilt, folgt:
$\begin{array}{l}x+2\ge 0\\ x\ge -2\end{array}$

Damit gilt für den Definitionsbereich der Funktion $f$: $D_f=\left\{x\text{:}x\in ℝ\wedge x\ge -2\right\}$.
Berechnung der Nullstellen ergibt:
$\begin{array}{l}{x}^3+2x^2=0\\ x^2\left(x+2\right)=0\end{array}$

Daraus folgt $x^2=0$ und somit $x_1=0$ bzw. $x+2=0$ und damit $x_2=-2$.
Der Graph der Funktion bestätigt das Ergebnis: Die Funktion hat zwei Nullstellen, und zwar $x_1=0$ und $x_2=-2$.

Exponentialfunktionen

Funktionen mit einer Gleichung der Form
$\begin{array}{l}f\left(x\right)=a^x\text{bzw}.\\ f\left(x\right)=c\cdot a^x(\text{mit}a,c,x\in ℝ;a>0;a\ne 1)\end{array}$
heißen Exponentialfunktionen zur Basis $a$.

Die Graphen der „reinen“ Exponentialfunktionen verlaufen immer oberhalb der $x$-Achse (diese Achse ist waagerechte Asymptote), d.h., sie besitzen keine Nullstellen. Wegen $a^0=1$ für alle $a$, verlaufen die Graphen alle durch den Punkt $\left(0;1\right)$ auf der $y$-Achse.

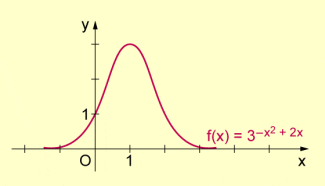
Auch bei Funktionen des Typs $f\left(x\right)=a^{h\left(x\right)}$ spricht man in weitem Sinne von Exponentialfunktionen (obwohl es sich eigentlich um eine Verkettung zweier Funktionen handelt). Funktionen dieses Typs, wie z.B. $f\left(x\right)=3^{-x^2+2x}$, besitzen ebenfalls keine Nullstellen.

In „nicht reinen“ Exponentialfunktionen kann es Nullstellen geben, wie das folgende Beispiel zeigt.

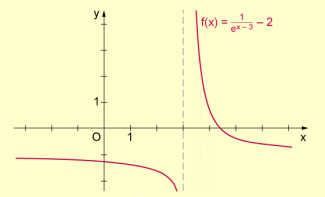
• Beispiel 2: Die Funktion $f(x)=e^{\frac{1}{x-3}}-2$ ist auf Nullstellen zu untersuchen.

Der Definitionsbereich dieser Funktion ist $D_f=ℝ\backslash \left\{3\right\}$.
Die Funktion ist an der Stelle $x_0=3$ nicht definiert; sie hat an dieser Stelle eine Definitionslücke.
Um mögliche Nullstellen zu ermitteln setzt man $f\left(x\right)=0$, d.h.:
$e^{\frac{1}{x-3}}-2=0$
Durch Logarithmieren erhält man
$\frac{1}{x-3}\cdot \ln e=\ln 2$
und wegen $\ln e=1$ demzufolge
$x=\frac{1}{\ln 2}+3\approx \mathrm{4,44}$
Diese Funktion hat also eine Nullstelle bei $x_1\approx \mathrm{4,44}$.

Logarithmusfunktionen

Logarithmusfunktionen sind die Umkehrfunktionen der Exponentialfunktionen bei gleicher Basis, mit einer Gleichung der folgenden Form:
$f\left(x\right)={\log }_{a}x(a,x\in ℝ;a>0; \; x \; > 0;a\ne 1)$

Die Graphen der Logarithmusfunktionen entstehen demnach durch Spiegelung der Graphen der zugehörigen Exponentialfunktionen an der Geraden $y=x$.
Damit ist klar: Alle „reinen“ Logarithmusfunktionen besitzen eine Nullstelle für $x_0=1$. In anderen Fällen müssen entsprechende Untersuchungen durchgeführt werden.

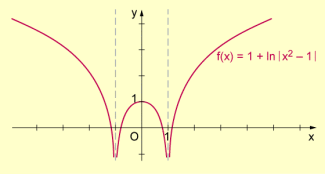
• Beispiel 3: Die Funktion $f(x)=1+\ln \left|x^2-1\right|$ ist auf Nullstellen zu untersuchen.

Da der Term $x^2-1$ für $x_1=1$ und $x_2=-1$ gleich null wird, hat die Funktion an diesen Stellen Definitionslücken, denn die Logarithmusfunktionen sind für den Wert Null nicht definiert. Damit ist der Definitionsbereich der Funktion $f$ gleich der Menge der reellen Zahlen ohne die Zahlen $-1$ und $1$, d.h., es ist $D_f=ℝ\backslash \left\{-1;1\right\}$.

Für die Berechnung der Nullstellen setzt man wieder $f\left(x\right)=0$ und erhält:
$\begin{array}{l}0=1+\ln \left|x^2-1\right|\text{bzw}.\\ \ln \left|x^2-1\right|=-1\end{array}$

Potenziert man beide Seiten dieser Gleichung zur Basis $e$, so ergibt sich:
$\begin{array}{l}{e}^{\ln \left|x^2-1\right|}=e^{-1}\\ \left|x^2-1\right|=e^{-1}\end{array}$

Auflösen des absoluten Betrages führt zu
$x^2-1=e^{-1}\text{bzw}.-(x^2-1)=e^{-1}$
und
$x^2=1+e^{-1}$ sowie $x^2=1-e^{-1}.$

Es muss also gelten:
$\left|x\right|=\sqrt{1+e^{-1}}\text{und}\left|x\right|=\sqrt{1-e^{-1}}$

Daraus bestimmt man $x_1\approx -\mathrm{1,1696,}{x}_2\approx \mathrm{1,1696,}{x}_3\approx -\mathrm{0,7951,}{x}_4\approx \mathrm{0,7951}$ als die vier Nullstellen der Funktion $f(x)=1+\ln \left|x^2-1\right|$.