Satz des Pascal
Der von BLAISE PASCAL (1623 bis 1662) gefundene und nach ihm benannte Satz besagt (im allgemeinen Fall) Folgendes:
Ein Sechseck ist genau dann Sehnensechseck eines Kegelschnittes, wenn die Schnittpunkte gegenüberliegender Seiten auf einer Geraden liegen.
Diese Gerade heißt pascalsche Gerade des Sechsecks.
BLAISE PASCAL (1623 bis 1662) lebte und arbeitete vorzugsweise in Paris. Schon als 13-Jähriger beschäftigte er sich selbstständig mit mathematischen Problemen, insbesondere den Elementen des EUKLID und der damals stark diskutierten Lehre von den Kegelschnitten.
Zusammen mit PIERRE DE FERMAT gilt PASCAL als Begründer der Kombinatorik. Nach ihm ist das pascalsche Dreieck (1654) benannt, das die Berechnung von Binomialkoeffizienten erleichtert. Auch konstruierte er eine Additionsmaschine, die er aber nicht weiterentwickelte.
Den nach ihm benannten (und im Folgenden angeführten) Satz über Sehnensechsecke fand PASCAL im Jahre 1640.
- Verlängert man in einem Sehnensechseck eines Kreises je zwei gegenüberliegende Seiten bis zum Schnitt, so liegen die Schnittpunkte auf einer Geraden.
-
Figur zum Satz des Pascal
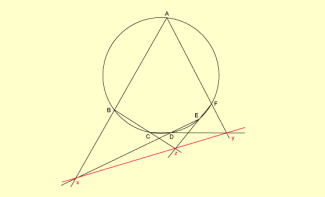
Gegenüberliegende Seiten und ihre Schnittpunkte sind hier:
Die Gerade durch X, Y und Z wird auch pascalsche Gerade genannt.
Zum Beweis des Satzes greift man auf Aussagen darüber zurück, unter welchen Bedingungen drei Punkte auf einer Geraden liegen (kollinear sind). Eine solche Auskunft gibt die Umkehrung des Satzes von MENELAOS. Man wird also versuchen, in der Sechseckfigur ein Dreieck zu erzeugen, das die Anwendung des Satzes von MENELAOS und seiner Umkehrung ermöglicht.
Man verlängert z.B. die nicht aneinander stoßenden Seiten , und , bis sie sich in den Punkten M, N und P schneiden.
Nach dem Satz über Sekantenabschnitte am Kreis gilt:
Wird das Dreieck MNP von den Geraden XA, YC und ZF geschnitten, so gelten nach dem Satz von MENELAOS folgende Relationen:
![]()
Man stelle sich vor, alle linken Seiten der Gleichungen (1) bis (6) und ebenso alle rechten Seiten seien miteinander multipliziert und bildeten so eine einzige Gleichung, auf deren Seiten alle die Faktoren stünden, die in den Gleichungen (1) bis (6) vorkommen. Dann könnte man diese Gleichung durch die Faktoren dividieren, die beide Seiten gemeinsam haben. Das ist erlaubt, denn alle vorkommenden Faktoren sind von null verschieden vorausgesetzt. Man muss aber die Gleichung mit den umfangreichen Seiten nicht aufschreiben – das Dividieren der auf beiden Seiten gemeinsam vorkommenden Faktoren kann man gleich an den Gleichungen (1) bis (6) vornehmen. So erkennt man z.B., dass in (1) auf der linken Seite der Faktor vorkommt, der in (4) rechts steht. Durch Dividieren wird er eliminiert.
Bearbeitet man alle sechs Gleichungen auf diese Weise, bleibt schließlich folgende Gleichung stehen:
Nach der Umkehrung des Satzes von MENELAOS bedeutet dies: Die Punkte X, Y und Z liegen auf einer Geraden.
Anmerkung: Der Satz wurde hier für ein Sehnensechseck beweisen, das einem Kreis einbeschrieben ist. Er gilt jedoch allgemein für Sehnensechsecke, die in einem beliebigen Kegelschnitt liegen.

