Ähnlichkeit von Dreiecken
Zwei Dreiecke sind zueinander ähnlich, wenn die entsprechenden Seiten gleiche Streckenverhältnisse bilden und die einander entsprechenden Winkel gleich groß sind.
Zwei Dreiecke sind zueinander ähnlich, wenn die entsprechenden Seiten gleiche Streckenverhältnisse bilden und die einander entsprechenden Winkel gleich groß sind.
-
Ähnliche Dreiecke

(c) Duden Learnattack
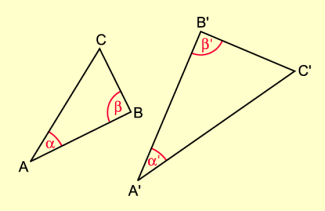
Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln übereinstimmen (Hauptähnlichkeitssatz).
ww:
Da die Winkelsumme im Dreieck immer 180° beträgt, stimmen die Dreiecke auch im dritten Winkel überein. Die Streckenverhältnisse brauchen nicht berücksichtigt zu werden.
-
Hauptähnlichkeitssatz
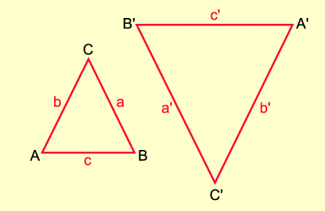
Zwei Dreiecke sind zueinander ähnlich, wenn sie in den Streckenverhältnissen aller entsprechender Seiten übereinstimmen.
sss:
-
Ähnlichkeitssatz sss
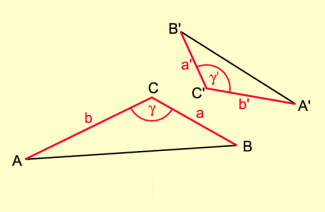
Zwei Dreiecke sind zueinander ähnlich, wenn sie in den Streckenverhältnissen zweier Seiten und dem jeweils eingeschlossenen Winkel übereinstimmen.
sws:
-
Ähnlichkeitssatz sws
Zwei Dreiecke sind zueinander ähnlich, wenn sie in den Streckenverhältnissen zweier Seiten und dem Winkel übereinstimmen, der jeweils der größeren Seite gegenüberliegt.
SsW:
-
Ähnlichkeitssatz SsW
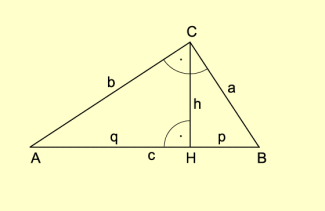
Anwendung finden die Ähnlichkeitssätze für Dreiecke vorwiegend beim Beweisen. So erfolgt einer der zahlreichen Beweise für den Satz des Pythagoras über die Ähnlichkeit von Dreiecken. Da im rechtwinkligen Dreieck die durch die Höhe über der Hypotenuse gebildeten Teildreiecke untereinander und dem Gesamtdreieck ähnlich sind, gilt:
und
So ergibt sich durch Addition der Beziehungen
Was zu zeigen war.
-
Rechtwinkliges Dreieck