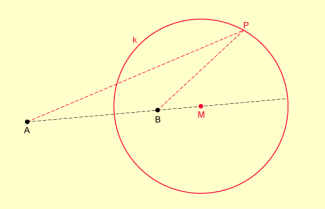
Apollonioskreis
Die Menge aller der Punkte P (einer Ebene), die von einem festen Punkt A doppelt so weit entfernt sind, wie von einem zweiten festen Punkt B, liegt auf einem Kreis, dem sogenannten Apollonios-Kreis.
Der griechische Geometer APOLLONIOS VON PERGE (um 262 bis etwa 190 v. Chr.) beschäftigte sich intensiv mit Fragen der Form geometrischer Figuren.
Als speziellen geometrischen Ort untersuchte APOLLONIOS die Menge aller der Punkte P, die von einem gegebenen Punkt A doppelt so weit entfernt sind wie von einem anderen gegebenen Punkt B, d. h., für die gilt:
Er stellte fest, dass diese Punkte auf einem Kreis (dem sogenannten Apollonios-Kreis) liegen.
In der folgenden Abbildung ist der Sachverhalt in einem kartesischen Koordinatensystem dargestellt, wobei als feste Punkte die Punkte A(0; 0) und B(6; 0) gewählt worden. Für den Mittelpunkt M und den Radius r des Apollonios-Kreises k gilt in diesem Fall:
![]()
Apollonios-Kreis im kartesischen Koordinatensystem
Die Punkte A, B, M und der Kreispunkt C sind sogenannte harmonische Punkte, d. h. Punkte der harmonischen Teilung der Strecke (B ist der innere harmonische Teilpunkt, C der äußere harmonische Teilpunkt der Strecke), d. h., es gilt:
-
Apollonios-Kreis