Baumdiagramme
Mithilfe von Baumdiagrammen lassen sich Vörgänge, die aus mehreren Stufen (Teilvorgängen) bestehen, veranschaulichen. Das betrifft sowohl kombinatorische Probleme als auch mehrstufige Zufallsexperimente (Zufallsversuche).
Mithilfe von Baumdiagrammen lassen sich Vorgänge, die aus mehreren Stufen bestehen, veranschaulichen. Wie bei einem Baum können sich die „Äste“ auf einer bestimmten Stufe des Diagramms „verzweigen“. Die Zweige entsprechen dann den Ergebnissen des nächsten Teilvorgangs.
Jeder Weg durch das Baumdiagramm, der auch Pfad genannt wird, charakterisiert ein mögliches Ergebnis des mehrstufigen Vorgangs.
Beispiel:
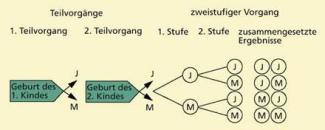
Die Geburt zweier Kinder kann als Zusammensetzung zweier nacheinander ablaufender Teilvorgänge angesehen werden. Jedes der beiden möglichen Ergebnisse (Junge oder Mädchen) des ersten Teilvorgangs ist mit jedem möglichen Ergebnis des zweiten Teilvorgangs kombinierbar. Bild 1 zeigt ein entsprechendes Baumdiagramm.
Ein Pfad eines Baumdiagramms heißt günstig für ein Ereignis E, wenn der diesem Pfad entsprechende Ablauf zu einem für dieses Ereignis günstigen Ergebnis führt. Ereignisse können durch mehrere Pfade repräsentiert werden.
Beispiel:
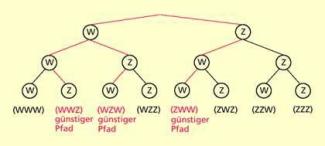
Eine Münze wird dreimal nacheinander geworfen. Als Ergebnis wird jeweils das Eintreffen von Wappen (W) oder Zahl (Z) betrachtet.
Im folgenden Baumdiagramm sind die für das Ereignis „Es fallen genau zwei Wappen“ günstigen Pfade hervorgehoben.Baumdiagramme können genutzt werden, um kombinatorische Probleme zu lösen, insbesondere alle möglichen Anordnungen von Elementen einer Menge zu erfassen.
Schreibt man bei mehrstufigen Zufallsexperimenten an die einzelnen Verzweigungen des Baumdiagramms die entsprechenden Wahrscheinlichkeiten für die Teilvorgänge, so kann man die Wahrscheinlichkeit von Ereignissen mithilfe der Pfadregeln berechnen.
-
Beispiel eines zweistufigen Vorgangs
-