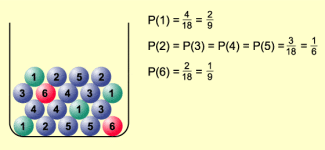Urnenmodell

Viele Probleme der klassischen Wahrscheinlichkeitsrechnung lassen sich mithilfe des Urnenmodells veranschaulichen (simulieren).

Das betrifft vor allem die sogenannten Grundaufgaben der Kombinatorik. Dazu wird angenommen, dass sich in einem Gefäß (der sogenannten Urne) n nummerierte (unterscheidbare) Kugeln befinden.
Eine Auswahl von k Elementen aus einer n-elementigen Grundmenge lässt sich durch Ziehen von k Kugeln realisieren. Man muss dabei zwischen einer Auswahl ohne und einer Auswahl mit Wiederholung unterscheiden. Im ersten Fall erfolgt die Ziehung ohne Zurücklegen, im zweiten Fall wird die jeweils gezogene Kugel wieder in die Urne zurückgelegt.

Auch Zufallsversuche, bei dem jedes mögliches Ergebnis die gleiche Wahrscheinlichkeit hat (Laplace-Experimente), lassen sich simulieren. Ein bestimmtes Ereignis (als Menge der dafür günstigen Ergebnisse) und die Wahrscheinlichkeit für das Eintreten dieses Ereignisses kann durch entsprechende Beschriftung (Nummerierung, Farbe usw.) der Kugeln definiert werden. Bild 1 zeigt das für die Simulation des Werfens eines „gezinkten“ Würfels.