Binomialkoeffizienten

Beim rechnerischen Lösen kombinatorischer Probleme bzw. beim Berechnen von Wahrscheinlichkeiten werden als Binomialkoeffizienten bezeichnete Terme verwendet. Es sind die Koeffizienten, die beim Entwickeln der n-ten Potenz eines Binoms (a + b) auftreten. Sie lassen sich aus dem sogenannten pascalschen Zahlendreieck gewinnen. Nachteil dabei ist jedoch, dass rekursiv verfahren wird, d. h., zur Ermittlung der Koeffizienten von ${\left(a+b\right)}^n$ müssen die von ${\left(a+b\right)}^{n-1}$ bekannt sein. Vorteilhafter ist deshalb die folgende Definition:

Unter dem Binomialkoeffizienten $\left(\begin{array}{c}n\\ k\end{array}\right)$ (gesprochen: n über k) versteht man den folgenden Ausdruck:
$\left(\begin{array}{c}n\\ k\end{array}\right)=\frac{n\cdot \left(n-1\right)\cdot \left(n-2\right)\cdot \mathrm{...}\cdot \left[n-\left(k-1\right)\right]}{1\cdot 2\cdot 3\cdot \mathrm{...}\cdot k}\text{mit }n,k\in \mathbb{N}\text{ und }n\ge k$
Es ist $\left(\begin{array}{c}n\\ 0\end{array}\right)=1$.
Hinweis: Die Anzahl der Faktoren in Zähler und Nenner eines Binomialkoeffizienten ist gleich.

Beispiele:
$\left(\begin{array}{c}10\\ 3\end{array}\right)=\frac{10\cdot 9\cdot 8}{1\cdot 2\cdot 3}=120\left(\begin{array}{c}90\\ 2\end{array}\right)=\frac{90\cdot 89}{1\cdot 2}=4005$

Mithilfe der Fakultätsschreibweise lässt sich die Definition der Binomialkoeffizienten auch folgendermaßen angeben:
$\left(\begin{array}{c}n\\ k\end{array}\right)=\frac{n!}{k!\cdot \left(n-k\right)!}\text{mit }n,k\in N\text{ und }n\ge k$
Unmittelbar zu erkennen ist, dass $\left(\begin{array}{c}n\\ 1\end{array}\right)=n$ gilt.

Zwei weitere Regeln für das Rechnen mit Binomialkoeffizienten lassen sich mithilfe des pascalschen Zahlendreiecks plausibel machen und unter Verwendung der allgemeinen Definition beweisen.

Eine erste Regel ergibt sich aus der symmetrischen Anordnung der Koeffizienten. Es gilt:
$\left(\begin{array}{c}n\\ k\end{array}\right)=\left(\begin{array}{c}n\\ n-k\end{array}\right)$
Mit dieser Regel lassen sich vorteilhaft Binomialkoeffizienten mit großem k, speziell für$k>\frac{n}{2}$ berechnen.

Beispiel:

$\left(\begin{array}{c}50\\ 48\end{array}\right)=\left(\begin{array}{c}50\\ 2\end{array}\right)=\frac{50\cdot 49}{1\cdot 2}=1225$

Des Weiteren erhält man im pascalschen Zahlendreieck die jeweiligen Zahlen einer Zeile, indem man die beiden darüber stehenden Zahlen addiert. Allgemein gilt:
$\left(\begin{array}{c}n\\ k\end{array}\right)+\left(\begin{array}{c}n\\ k+1\end{array}\right)=\left(\begin{array}{c}n+1\\ k+1\end{array}\right)$

$$Beispiel:

$\left(\begin{array}{c}6\\ 3\end{array}\right)+\left(\begin{array}{c}6\\ 4\end{array}\right)=\left(\begin{array}{c}7\\ 4\end{array}\right)$

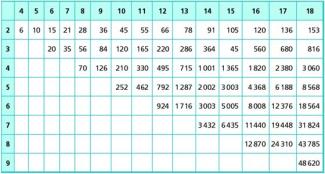
In der Tabelle von Bild 1 sind die Binomialkoeffizienten (die mittels einer speziellen Taste nCr bei vielen Taschenrechnern auch direkt abgerufen werden können) bis n = 18 angegeben.

Mithilfe der Binomialkoeffizienten lässt sich der binomische Satz allgemein folgendermaßen formulieren.
Für alle reellen Zahlen a und b sowie für alle natürlichen Zahlen n gilt:
$\begin{array}{l}{\left(a+b\right)}^n=\left(\begin{array}{c}n\\ 0\end{array}\right)\cdot a^n+\left(\begin{array}{c}n\\ 1\end{array}\right)\cdot a^{n-1}b+\left(\begin{array}{c}n\\ 2\end{array}\right)\cdot a^{n-2}{b}^2+\mathrm{...}\\ \mathrm{...}+\left(\begin{array}{c}n\\ n-1\end{array}\right)\cdot a{b}^{n-1}+\left(\begin{array}{c}n\\ n\end{array}\right)\cdot b^n\end{array}$

bzw. unter Verwendung des Summenzeichens
${\left(a+b\right)}^n={\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)}\cdot a^{n-k}{b}^k$

Beispiel:
Es ist das dritte Glied der Entwicklung von 

${\left(a+b\right)}^{10}$ anzugeben.

Lösung: $\left(\begin{array}{c}10\\ 2\end{array}\right)\cdot a^{10-2}{b}^2=45a^8{b}^2$