Beweise, Allgemeines

Beweisverfahren

Man unterscheidet im Wesentlichen zwei Beweisverfahren, den direkten Beweis und den indirekten Beweis.
Jeder Beweis besteht aus drei Schritten, die schon von EUKLID so angegeben wurden, nämlich
Voraussetzung - Behauptung - Beweis(durchführung).
Die Beweisdurchführung verlangt, eine endliche Kette wahrer Aussagen (Folgerungen) aufzubauen, wobei beim Übergang von einem Glied der Folgerungskette zum nächsten nur die Voraussetzung, bereits bewiesene Sätze, Gesetze der Logik (Schlussregeln) und Regeln für äquivalente Umformungen verwendet werden dürfen. Insbesondere ist streng darauf zu achten, dass nicht die Behauptung des Satzes (u. U. in anderer Formulierung, bereits umgeformt oder anderweitig „versteckt“) bei der Beweisdurchführung genutzt wird. Die Behauptung muss sich vielmehr als letztes Glied in der Folgerungskette ergeben.
Wenn eine mathematische Aussage bewiesen werden soll, dann ist es günstig, diese Aussage in Form einer Implikation, also in „wenn …, dann …“-(oder in „wenn … , so gilt …“-) Form anzugeben. Der auf „wenn“ folgende Satzteil enthält bei einer solchen Formulierung die Voraussetzung, der sich an „dann“ (bzw. „so gilt“) anschließende die Behauptung. Die Umkehrung eines Satzes lässt sich auf diese Weise ebenfalls leichter formulieren.

Direkter Beweis

Der Ausgangspunkt eines direkten Beweises sind bereits bewiesene Aussagen sowie die jeweiligen Voraussetzungen. Aus diesen wird dann mithilfe gültiger Schlussregeln nach einer endlichen Anzahl von Schritten die Behauptung gewonnen.

Indirekter Beweis

Bei der Durchführung des indirekten Beweises wird angenommen, dass die Negation der Behauptung gilt. Ausgehend von wahren Aussagen schließt man unter Nutzung gültiger Schlussregeln so lange, bis sich ein Widerspruch entweder zur Voraussetzung, zu bereits bewiesenen Sätzen, Definitionen oder zur Annahme (negierte Behauptung) ergibt. Tritt ein solcher Widerspruch ein, dann muss die negierte Behauptung falsch sein und es gilt die eigentliche Behauptung.
Lässt sich die Ausgangsannahme nicht zum Widerspruch führen, dann kann man mit dem indirekten Beweisverfahren die Gültigkeit des betreffenden Satzes nicht nachweisen.
Der indirekte Beweis wird oft zur Erkenntnissicherung bei Existenz- und Eindeutigkeitsaussagen, beim Beweisen von Satzumkehrungen und negierten Aussagen genutzt.
Im folgenden Beispiel wird sowohl das direkte als auch das indirekte Beweisverfahren angewendet:

Die Diagonalen in einem ebenen konvexen Viereck stehen genau dann senkrecht aufeinander, wenn die Summe der Maßzahlquadrate der Gegenseiten gleich ist.
In diesem Satz wird eine Aussage über beliebige (ebene und konvexe) Vierecke getroffen, es handelt sich um eine Allaussage und überdies um eine Äquivalenzaussage, sodass wir zwei Beweise führen müssen. Es ist nämlich zu beweisen:

(1) Wenn die Diagonalen im Viereck senkrecht aufeinander stehen, so ist die Summe der Maßzahlquadrate der Gegenseiten gleich:$\text{A}\Rightarrow \text{B}$
(2) Wenn im Viereck die Summe der Maßzahlquadrate der Gegenseiten gleich ist, so stehen die Diagonalen senkrecht aufeinander: $\text{B}\Rightarrow \text{A}$

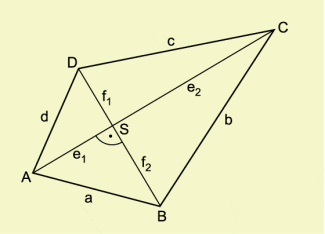
Um die Allaussage zu beweisen, genügt es, den Beweis für ein beliebiges ebenes konvexes Viereck zu führen. Eine Skizze, die allein natürlich noch nichts „beweist“, kann insbesondere bei geometrischen Sachverhalten helfen, Bezeichnungen festzulegen und Beweisideen schneller zu finden.

(1) Die Gültigkeit der ersten Implikation zeigen wir durch einen direkten Beweis:
Voraussetzung:
Viereck ABCD mit den Seiten a, b, c, d und den Diagonalen
$\left|\overline{\text{AC}}\right|=e=e{}_1+e{}_2\left|\overline{BD}\right|=f=f{}_1+f{}_{2}unde\perp f$
Behauptung: $a^2+c^2=b^2+d^2$
Beweis: Nach dem Satz des Pythagoras gilt für die rechtwinkligen Dreiecke ABS, BCS, CDS und ASD:
$\begin{array}{l}{\text{a}}^{\text{2}}=\text{e}{}_{\text{1}}^{\text{2}}+{\text{f}}_{\text{2}}^{\text{2}}\\ {\text{c}}^{\text{2}}={\text{f}}_{\text{1}}^{\text{2}}+{\text{e}}_{\text{2}}^{\text{2}}\\ {\text{a}}^{\text{2}}+{\text{c}}^{\text{2}}={\text{e}}_{\text{1}}^{\text{2}}+{\text{e}}_{\text{2}}^{\text{2}}+{\text{f}}_{\text{1}}^{\text{2}}+{\text{f}}_{\text{2}}^{\text{2}}\\ {\text{b}}^{\text{2}}={\text{e}}_{\text{2}}^{\text{2}}+{\text{f}}_{\text{2}}^{\text{2}}\\ {\text{d}}^{\text{2}}={\text{e}}_{\text{1}}^{\text{2}}+{\text{f}}_{\text{1}}^{\text{2}}\\ {\text{b}}^{\text{2}}+{\text{d}}^{\text{2}}={\text{e}}_{\text{1}}^{\text{2}}+{\text{e}}_{\text{2}}^{\text{2}}+{\text{f}}_{\text{1}}^{\text{2}}+{\text{f}}_{\text{2}}^{\text{2}}\end{array}$
Ein Vergleich der beiden Seiten zeigt: $a^2+c^2=b^2+d^2$ w. z. b. w.

(2) Der Beweis für die zweite Implikation erfolgt indirekt:

Voraussetzung:
Viereck ABCD mit den Seiten a, b, c, d und den Diagonalen
$\left|\overline{\text{AC}}\right|=e=e{}_1+e{}_2\left|\overline{BD}\right|=f=f{}_1+f{}_{2}und{a}^2+c^2=b^2+d^2$

Behauptung: $e\perp f$
Beweis (indirekt): Wir nehmen an, es seien e und f nicht senkrecht zueinander.
Dann kann man von A bzw. C das Lot auf die Diagonale fällen und erhält die Höhen mit den Fußpunkten E bzw. F.
In den rechtwinkligen Dreiecken ABE, FCD, FBC und AED gilt nach dem Satz des Pythagoras:
$\begin{array}{l}{\text{a}}^{\text{2}}={\text{h}}_{\text{1}}^{\text{2}}+{\left(y+\text{z}\right)}^{\text{2}}={\text{h}}_{\text{1}}^{\text{2}}+{\text{z}}^{\text{2}}+{\text{y}}^{\text{2}}+\text{2zy}\\ {\text{c}}^{\text{2}}={\text{h}}_{\text{2}}^{\text{2}}+{\left(\text{x}+\text{y}\right)}^{\text{2}}={\text{h}}_{\text{2}}^{\text{2}}+{\text{x}}^{\text{2}}+{\text{y}}^{\text{2}}+\text{2xy}\\ {\text{a}}^{\text{2}}+{\text{c}}^{\text{2}}={\text{h}}_{\text{1}}^{\text{2}}+{\text{h}}_{\text{2}}^{\text{2}}+{\text{x}}^{\text{2}}+{\text{z}}^{\text{2}}+\text{2y}\left(\text{x}+\text{y}+\text{z}\right)\\ {\text{b}}^{\text{2}}={\text{h}}_{\text{2}}^{\text{2}}+{\text{z}}^{\text{2}}\\ {\text{d}}^{\text{2}}={\text{h}}_{\text{1}}^{\text{2}}+{\text{x}}^{\text{2}}\\ {\text{b}}^{\text{2}}+{\text{d}}^{\text{2}}={\text{h}}_{\text{1}}^{\text{2}}+{\text{h}}_{\text{2}}^{\text{2}}+{\text{x}}^{\text{2}}+{\text{z}}^{\text{2}}\end{array}$
Ein Vergleich zeigt, dass ${\text{a}}^{\text{2}}+{\text{c}}^{\text{2}}\ne {\text{b}}^{\text{2}}+{\text{d}}^{\text{2}}$ nur gilt, wenn $y\ne 0$ gilt.
Letzteres folgt aber aus der Annahme, dass e nicht senkrecht zu f sei.
Damit liegt ein Widerspruch zur Voraussetzung
(${\text{a}}^{\text{2}}+{\text{c}}^{\text{2}}={\text{b}}^{\text{2}}+{\text{d}}^{\text{2}}$) vor.
Das heißt: Die Annahme „e ist nicht senkrecht zu f“ ist falsch.
Nach dem Schluss auf eine Negation ist demzufolge die Behauptung $e\perp f$ wahr. w. z. b. w.
Aus der Wahrheit der Implikationen folgt die Wahrheit der Aussage $A\iff B$. w. z. b. w.