Bruchungleichungen, Lösen

Ungleichungen, die Bruchterme enthalten, werden Bruchungleichungen genannt.
Ein Beispiel für eine Bruchungleichung ist: $\frac{\text{x}+\text{2}}{\text{x}-\text{5}}>\text{0}$
Um alle Lösungen dieser Bruchungleichung zu finden, müssen zwei Fälle unterschieden werden, denn es gibt zwei Möglichkeiten, damit ein Bruch größer als null ist:

      1. Fall: Der Zähler und der Nenner sind beide größer als null.
      2. Fall: Der Zähler und der Nenner sind beide kleiner als null.

Beide Fälle müssen untersucht werden, um alle Lösungen der Bruchungleichung zu finden.

1. Fall: Zähler und Nenner sind beide positiv.
$\begin{array}{l}\text{x}+\text{2}>\text{0}\wedge \text{x}-\text{5}>\text{0}\\ x>-2\wedge x>5\end{array}$
Lösungen sind alle Zahlen, die gleichzeitig größer als –2 und größer als 5 sind. Das sind alle Zahlen, für die x > 5 gilt.

2. Fall: Zähler und Nenner sind beide negativ.
$\begin{array}{l}\text{x}+\text{2}<\text{0}\wedge \text{x}-\text{5}<\text{0}\\ x<-2\wedge x<5\end{array}$
Lösungen sind alle Zahlen, die gleichzeitig kleiner als –2 und kleiner als 5 sind. Das sind alle Zahlen, für die x < –2 gilt.

Lösungen für die Bruchungleichung sind also alle x,
für die x > 5 oder x < –2 gilt.
$\text{L}=\left\{\text{x}\in \text{Q}|\text{x}<-\text{2}\vee \text{x}>\text{5}\right\}$
Bei x = –2 wird der Zähler null und der Nenner ist nicht null. Also hat der Bruchterm den Wert null.
Bei x = 5 wird der Nenner null, dort ist der Bruchterm also nicht definiert.

Weiterführende Betrachtungen

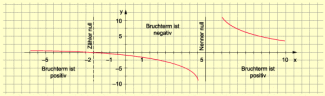
Der Bruchterm ist für alle Zahlen, die größer als –2 und kleiner als 5 sind, negativ.
Eine übersichtliche Zusammenfassung der Ergebnisse erhält man, wenn man die Bruchgleichung als Funktionsgleichung $\text{y}=\frac{\text{x}+\text{2}}{\text{x}-\text{5}}$ betrachtet, eine Wertetabel le berechnet und diese in einem Koordinatensystem darstellt.