Diagonalverfahren
Obwohl die Menge der gebrochenen Zahlen unendlich und überall dicht ist, kann man die gebrochenen Zahlen eindeutig den natürlichen Zahlen zuordnen, man kann sie abzählen.
Die Menge der gebrochenen Zahlen ist abzählbar. Dies geschieht nach dem sogenannten cantorschen Diagonalverfahren (benannt nach GEORG CANTOR, 1845 bis 1918).
Obwohl die Menge der gebrochenen Zahlen unendlich und überall dicht ist, kann man die gebrochenen Zahlen eindeutig den natürlichen Zahlen zuordnen, man kann sie abzählen.
Die Menge der gebrochenen Zahlen ist abzählbar. Dies geschieht nach dem sogenannten cantorschen Diagonalverfahren (benannt nach GEORG CANTOR, 1845 bis 1918) wie folgt:
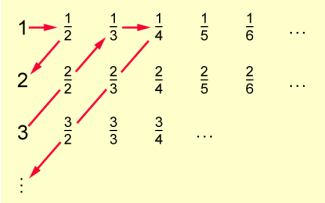
Die gebrochenen Zahlen werden nach nebenstehendem Schema angeordnet. Dabei werden offensichtlich alle erfasst. Man zählt nun von 1 beginnend in Pfeilrichtung und lässt dabei alle Brüche, die eine schon erfasste gebrochene Zahl darstellen, weg. Die Reihenfolge lautet also:
Man hat die gebrochenen Zahlen abgezählt, allerdings nicht mehr in einer der Größe nach geordneten Reihenfolge dargestellt.
-
Diagonalverfahren