Funktionen, Parameterdarstellung
Üblicherweise werden Funktionen durch die Angabe geordneter Paare, durch eine Wortvorschrift, durch Wertetabellen, durch Funktionsgleichungen oder durch grafische Darstellungen beschrieben. Teilweise nutzt man auch die sogenannte Parameterdarstellung. Sie ist dadurch gekennzeichnet, dass die Variable x und auch die Variable y jeweils durch eine Funktionsgleichung beschrieben werden, die einen (gemeinsamen) Parameter t als unabhängige Variable enthält.
Üblicherweise werden Funktionen durch die Angabe geordneter Paare, durch eine Wortvorschrift, durch Wertetabellen, durch Funktionsgleichungen oder durch grafische Darstellungen beschrieben. Teilweise nutzt man auch die sogenannte Parameterdarstellung. Sie ist dadurch gekennzeichnet, dass die Variable x und auch die Variable y jeweils durch eine Funktionsgleichung beschrieben werden, die einen (gemeinsamen) Parameter t als unabhängige Variable enthält. In einer solchen Darstellung lassen sich Kurven beschreiben, die durch den bisher verwendeten Funktionsbegriff nicht erfasst sind.
Beispiel:
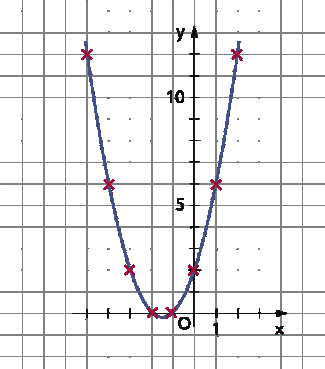
Eine Funktion f ist durch die zwei Gleichungen x = f1(t) = t – 1 und y = f2(t) = t² + t mit t gegeben. Für das Intervall –4 ≤ t ≤ 3 erhält man folgende Wertetabelle:
| t | –4 | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| x = t – 1 | –5 | –4 | –3 | –2 | –1 | 0 | 1 | 2 |
| y = t² + t | 12 | 6 | 2 | 0 | 1 | 2 | 6 | 12 |
Die Eintragung der Zahlenpaare (x | y) in ein Koordinatensystem ergibt eine Parabel (Bild 1).
Betrachtet man beide Parametergleichungen als Gleichungssystem und isoliert den Parameter t, erhält man eine parameterfreie Funktionsgleichung, die denselben Graphen liefert:
| Parametergleichungen: | I x = t – 1 II y = t² + t | |
| Auflösen von Gleichung I nach t: | I’ t = x + 1 | |
| Einsetzen von I’ in II: | y = (x + 1)² + (x + 1) y = x² + 3x + 2 | |
| Parameterfreie Funktionsgleichung: | y = f(x) = x² + 3x + 2 |
Beispiel:
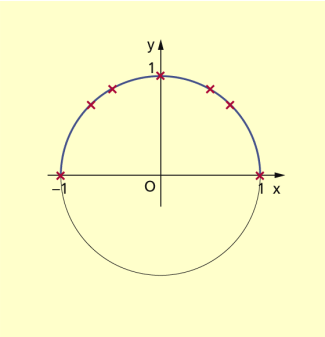
Durch die Gleichung x = f2(t) = cos t und y = f2(t) = sin t
mit 0 ≤ t ≤![]() ist eine Funktion gegeben, für die man folgende Wertetabelle erhält:
ist eine Funktion gegeben, für die man folgende Wertetabelle erhält:
| t | 0 | ||||||
| x = cos t | 1 | 0 | – | – | –1 | ||
| y = sin t | 0 | 1 | 0 |
-
Parabel
Die Eintragung der Koordinatenpaare (x | y) in ein Koordinatensystem lässt die Vermutung zu, dass durch die beiden Parametergleichungen eine Funktion beschrieben wird, deren Graph ein Halbkreis ist (Bild 2).
Die Fortsetzung der Tabelle für den II. und III. Quadranten würde sogar einen Kreis entstehen lassen. Da der Kreis keine eindeutige Abbildung ist, darf er jedoch nicht als Funktionsgraph interpretiert werden.
Um parametrische Kurven mit dem Programm Derive zu erstellen, werden die Funktionsterme für x und y in eckiger Klammer (als Matrix) eingegeben:
#1: [cos(t), sin (t)]
Wird die Schaltfläche „Ausdruck zeichnen“ im Grafik-Fenster betätigt, erscheint ein Dialog zur Eingabe des Intervalls des Parameters t.
Der für 0 ≤ t ≤ entstehende Halbkreis ist noch verzerrt und kann über „Einstellen/Verzerrrungsverhältnis/Rücksetzen“ korrigiert werden. Auf die gleiche Art und Weise wird
für 0 ≤ t ≤ 2 ein Kreis dargestellt.
![]()
Durch geeignete Gleichungen und Parameterbereiche lassen sich interessante Kurven darstellen, die ohne Computerprogramme kaum möglich wären.
Beispiele:
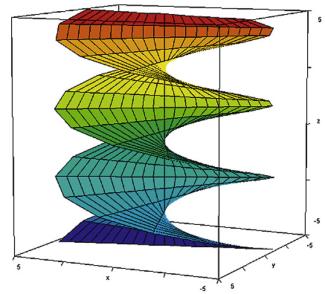
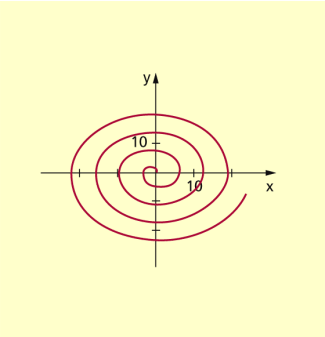
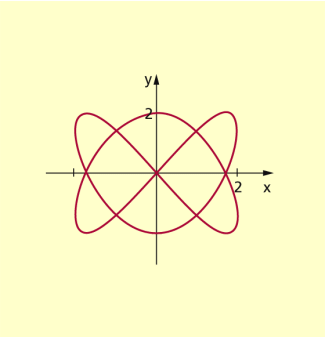
| Archimedische Spirale | Lissajous-Figuren | Raumkurven |
| x = t · cos t y = t · sin t | x = 2 · sin 2t y = 2 · sin 3t | x = k · sin t y = k · cos t; z = t |
| 0 ≤ t ≤ 8 | 0 ≤ t ≤ 2 | 0 ≤ t ≤ 2 |
| (Bild 3) | (Bild 4) | (Bild 5) |
-
Halbkreis
-
Archimedische Spirale
-
Lissajous-Figuren
-
Raumkurven