Kugel

Die Kugel ist die Menge aller Punkte des Raums, die von einem festen Punkt M, dem Mittelpunkt der Kugel, den gleichen Abstand r haben. Der Abstand heißt Radius der Kugel.

Die Kugel ist ein Rotationskörper. Sie entsteht, wenn ein Halbkreis um seinen Durchmesser rotiert. Der Kreismittelpunkt ist zugleich Kugelmittelpunkt.

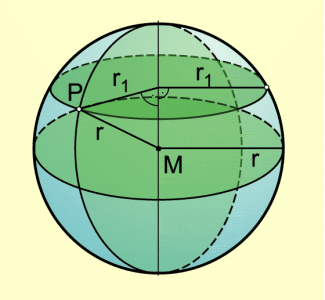
Jeder ebene Schnitt durch den Kugelmittelpunkt ergibt einen Großkreis mit demselben Mittelpunkt M und Radius r. Auf einem Globus sind das der Äquator und die Meridiane. Alle anderen ebenen Schnittfiguren sind Kreise mit kleineren Radien. Sie werden Breitenkreise genannt. Ihre Radien sind kleiner als der Kugelradius.
Nach einer Idee von GALILEO GALILEI lässt sich das Volumen einer Halbkugel über einen Vergleichskörper herleiten. Der Vergleichskörper entsteht, wenn man aus einem Zylinder mit den Grundflächenradius r und der Höhe h einen Kreiskegel mit gleicher Grundfläche und Höhe herausschneidet. Für das Volumen einer Kugel mit dem Radius r gilt:
$V=\frac{4}{3}\pi r^3$

Die Oberfläche eines Fußballs ist aus regelmäßigen Fünfecken und Sechsecken zusammengesetzt. Verbindet man alle Ecken dieser Flächen mit dem Kugelmittelpunkt des Balls, so wird dieser näherungsweise in Pyramiden aufgeteilt, die alle als Höhe den Kugelradius haben. Eine derartige Zerlegung ist mit jeder Kugel denkbar. Die Annäherung wird mit zunehmender Anzahl der Teilflächen immer besser.
Der Inhalt der Kugeloberfläche $A_O$ist folglich gleich der Summe aller Grundflächen der Pyramiden:
$A_O=A_{G,1}+A_{G,2}+A_{G,3}+\mathrm{...}+A_{G,n}$

Das Volumen der Kugel setzt sich aus den Volumina der Pyramiden zusammen:
$V=\frac{1}{3}{A}_{G,1}\cdot r+\frac{1}{3}{A}_{G,2}\cdot r+\mathrm{...}+\frac{1}{3}{A}_{G,n}\cdot r=\frac{1}{3}{A}_O\cdot r$

Aus obiger Gleichung und $V=\frac{4}{3}\pi r{}^3$
folgt: $A_O=4\pi r{}^2$

Für den Oberflächeninhalt einer Kugel mit dem Radius r gilt:
$A_O=4\pi r{}^2$