Monotonie

Bei der Untersuchung von Funktionen und ihren Anwendungen kann es von Interesse sein zu ermitteln, wie sich die Funktionswerte mit wachsenden Argumenten verändern bzw. wie der Graph der Funktion verläuft, wenn die x-Werte seiner Punkte größer werden.

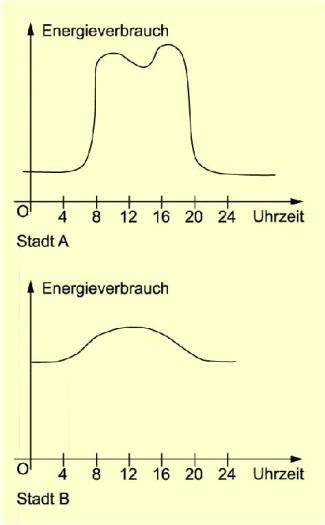
Geben die beiden Diagramme in Bild 1 etwa den Elektroenergieverbrauch zweier Städte A und B (die sich vor allem hinsichtlich Art und Anzahl der dort ansässigen Industriebetriebe unterscheiden) im Verlaufe von 24 Stunden eines Werktages vereinfacht wieder, so kann man daraus u. a. entnehmen:

• Im (oberen) Diagramm der Stadt A ist in der Zeit zwischen 0 und 4 Uhr der Energieverbrauch auf niedrigem Niveau nahezu konstant (Hauptabnehmer arbeiten nicht), wächst aber ab ca. 5 Uhr rasch an, bleibt dann (abgesehen von einer Verringerung in der Mittagszeit) wiederum nahezu gleich und fällt am späten Nachmittag bzw. frühen Abend rasch auf das „Nachtniveau“ ab.
• Im (unteren) Diagramm der Stadt B ist in der Zeit zwischen 0 und 4 Uhr der Energieverbrauch ebenfalls nahezu konstant, allerdings auf hohem Niveau (Hauptabnehmer arbeiten im Drei-Schicht-Betrieb), wächst danach allmählich (durch den Haushaltsbedarf und weitere Betriebe) an, bleibt dann nahezu gleich und fällt ab etwa 16 Uhr allmählich auf das „Nachtniveau“ ab.

Als Verallgemeinerung der in obigem Beispiel verwendeten Beschreibungen des Diagrammverlaufs gelangen wir zum Begriff der Monotonie einer Funktion:

• Eine Funktion f heißt in einem Intervall ihres Definitionsbereiches monoton wachsend (steigend), wenn für alle $x_1$ und $x_2$ aus dem Intervall gilt:
  Aus $x_1<x_2$ folgt stets $f\left(x_1\right)\le f\left(x_2\right)$.
  Gilt dabei sogar $f\left(x_1\right)<f\left(x_2\right)$, so spricht man einer streng monoton wachsenden (steigenden) Funktion.
• Eine Funktion f heißt in einem Intervall ihres Definitionsbereiches monoton fallend, wenn für alle $x_1$ und $x_2$ aus dem Intervall gilt:
  Aus $x_1<x_2$ folgt stets $f\left(x_1\right)\ge f\left(x_2\right)$.
  Gilt dabei sogar $f\left(x_1\right)>f\left(x_2\right)$, so spricht man einer streng monoton fallenden Funktion.

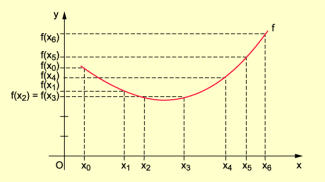
Will man das Monotonieverhalten einer gegebene Funktion in einem bestimmten Intervall rechnerisch untersuchen, so muss man entsprechend obiger Definition die Funktionswerte für wachsende Argumente miteinander vergleichen. Die Zuverlässigkeit der dadurch gewonnenen Aussagen hängt wesentlich von der gewählten „Schrittgröße“ ab. Würde man beispielsweise eine Funktion f mit dem in Bild 2 abgebildeten Graphen bezüglich Monotonie im Intervall $\left[x_0;x_6\right]$ nur durch Vergleich der Funktionswerte an den Stellen $x_1$, $x_4$ und $x_5$ untersuchen, so käme man evtl. zu dem Trugschluss, dass die Funktion dort durchgängig monoton wachsend wäre. Erst durch Einbeziehen der Stellen $x_2$ und $x_3$wird deutlich, dass dies so nicht zutrifft, sondern „feinere“ Untersuchungen erforderlich sind.

Eine detaillierte Untersuchung des Monotonieverhaltens einer Funktion kann mithilfe der Differenzialrechnung, konkret der 1. Ableitung vorgenommen werden.