Produktmenge

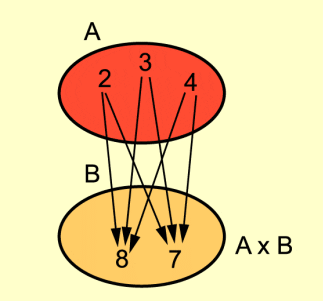
Die Produktmenge A x B (gesprochen: A kreuz B) ist die Menge aller geordneten Paare, deren erstes Element aus A und deren zweites Element aus B ist (Bild 1):
$A\times B=\left\{\left(x;y\right)\text{:}x\in A\wedge y\in B\right\}$
Die Produktmengenbildung ist nicht kommutativ.

Beispiel 1:
$\begin{array}{l}A=\left\{2;3;4\right\}B=\left\{7;8\right\}\\ A\times B=\left\{\left(2;7\right);\left(2;8\right);\left(3;7\right);\left(3;8\right);\left(4;7\right);\left(4;8\right)\right\}\\ B\times A=\left\{\left(7;2\right);\left(7;3\right);\left(7;4\right);\left(8;2\right);\left(8;3\right);\left(8;4\right)\right\}\end{array}$

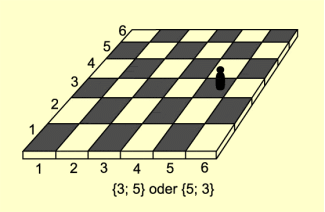
Beispiel 2:
In einem aus sechsunddreißig Feldern bestehenden quadratischen Spielfeld (6 x 6) werden die Felder am Rand senkrecht und waagerecht mit Ziffern versehen (Bild 2). Um die Lage des Spielsteins genau bestimmen zu können, ist es wichtig, die Reihenfolge bei der Angabe der Ziffern festzulegen.

Ein geordnetes Paar (a; b) entsteht durch Zusammenfassen zweier Elemente a und b in einer festen Reihenfolge. Sind a und b Zahlen, ist das geordnete Paar ein Zahlenpaar.
Geordnete Zahlenpaare werden z. B. zur Angabe der Position eines Punktes im ebenen kartesischen Koordinatensystem genutzt.

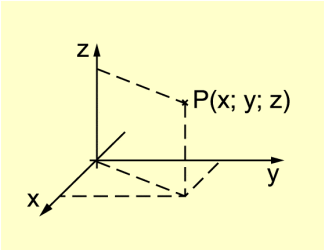
Wird die Produktmenge aus drei Zahlenmengen gebildet, so entstehen geordnete Zahlentripel (a; b; c).
Geordnete Zahlentripel werden z. B. zur Angabe der Position eines Punktes in einem räumlichen Koordinatensystem genutzt (Bild 3).