Sehnensatz

Schneiden in einem Kreis zwei Sehnen einander, so ist das Produkt der beiden Abschnitte auf der einen Sehne gleich dem Produkt der Abschnitte auf der anderen Sehne (Bild 1).

Beweis des Sehnensatzes
Voraussetzung:
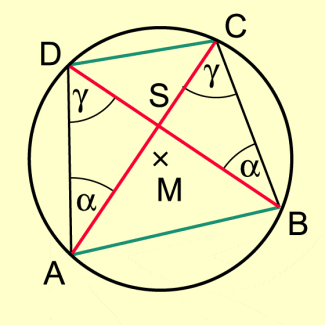
AC und BD sind zwei Sehnen im Kreis.
S ist Schnittpunkt der Sehnen.

Behauptung:
$\overline{AS}\cdot \overline{SC}=\overline{BS}\cdot \overline{SD}$

Beweis:
Die Strecken AB und CD sind auch Sehnen des Kreises,
also gilt $\sphericalangle BDA=\sphericalangle BCA$ und $\sphericalangle DBC=\sphericalangle DAC$ (Umfangswinkelsatz) und Dreieck ASD ist ähnlich Dreieck CSB (Hauptähnlichkeitssatz).
Damit gilt:
$\overline{AS}:\overline{BS}=\overline{SD}:\overline{SC}$ also auch $\overline{AS}\cdot \overline{SC}=\overline{BS}\cdot \overline{SD}$ (w. z. b. w.)

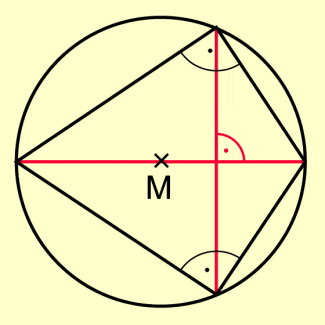
Für den Spezialfall, dass eine Sehne Durchmesser des Kreises und die andere Sehne dazu senkrecht ist, liegt ein rechtwinkliges Dreieck vor, weil nach dem Satz des Thales jeder Umfangswinkel über dem Durchmesser ein rechter Winkel ist (Bild 2).