Spezielle Wurzelfunktion
Besonders häufig treten Funktionen mit Gleichungen der Form auf. Die Funktion ist die Umkehrfunktion (inverse Funktion) zu , jedoch nur für , da die Gleichung keine umkehrbar eindeutige (eineindeutige) Zuordnung beschreibt.
Funktionen mit Gleichungen der Form heißen Wurzelfunktionen.
Besonders häufig treten Funktionen mit Gleichungen der Form auf. Die Funktion ist die Umkehrfunktion (inverse Funktion) zu , jedoch nur für , da die Gleichung keine umkehrbar eindeutige (eineindeutige) Zuordnung beschreibt.
-
a ist die n-te Wurzel aus c
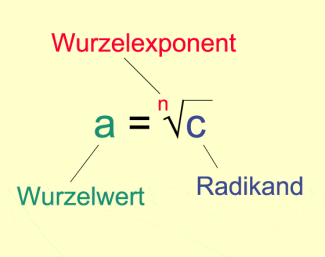
ist nicht äquivalent zu , da Quadrieren keine äquivalente Umformung darstellt. Zieht man auf beiden Seiten die Wurzel, dann erhält man nach der Quadratwurzeldefinition mit folgender Fallunterscheidung:
(1) , wenn
(2) , wenn .
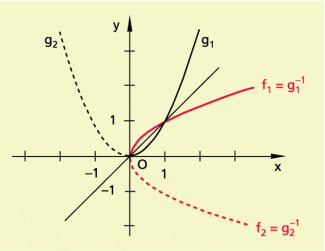
ist die Umkehrung von mit ,
ist die Umkehrung von mit (Bild 2).
-
Umkehrung der quadratischen Funktion