Vierteldifferenz
Die Vierteldifferenz bzw. Halbweite ist ein Streuungsmaß, das sich auf den Zentralwert
bezieht. Sie berechnet sich wie folgt aus dem unteren Viertelwert und oberen Viertelwert:
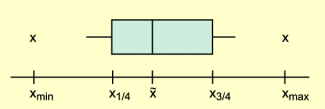
Die Halbweite gibt die Länge eines Boxplots an.
Die Vierteldifferenz bzw. Halbweite ist ein Streuungsmaß, das sich auf den Zentralwert bezieht.
Durch den Zentralwert wird eine Datenmenge in eine untere und obere Hälfte geteilt. Von diesen so entstandenen Datenmengen wird jeweils wieder der Zentralwert ermittelt. Der Zentralwert der unteren Hälfte wird als unterer Viertelwert, der der oberen Hälfte als oberer Viertelwert bezeichnet ( und können vorteilhaft Stängel-Blatt-Diagrammen entnommen werden). Mindestens die Hälfte aller Beobachtungswerte x liegt dann im Intervall , d. h., für diese x gilt:
Die Länge dieses Intervalls ist ein Maß für die Streuung der Häufigkeitsverteilung um den Zentralwert und wird als Halbweite bzw. Vierteldifferenz (Viertelabstand) H bezeichnet. Sie berechnet sich als
.
Die Halbweite gibt zugleich die Länge eines Boxplots an.
-
Boxplot