Addition von Geschwindigkeiten

Addition von Geschwindigkeiten in der klassischen Physik

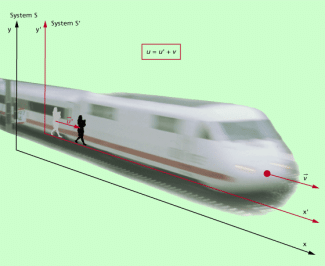
In der klassischen Physik addieren sich bei gleich gerichteten Bewegungen die Beträge der Geschwindigkeiten. Als Beispiel betrachten wir eine Person in einem Zug, der sich mit der Geschwindigkeit v in positiver x-Richtung bewegt (Bild 1). In dem Zug läuft eine Person in der gleichen Richtung mit der Geschwindigkeit u'. Das ist zugleich die Geschwindigkeit, die die Person im Bezugssystem S' hat, das sich mit dem Zug mitbewegt. Bezüglich eines mit dem Bahndamm verbundenen Bezugssystems S hat die Person dann die Geschwindigkeit

u = u' + v
Das ist das Gesetz für die klassische Addition von Geschwindigkeiten. Eine formale Anwendung dieses Gesetzes auf beliebige Geschwindigkeiten führt zu physikalisch nicht sinnvollen Ergebnissen: Beträgt z.B. u' = 0,6 c und v = 0,6 c, so würde man für u erhalten:
u = 0, 6 c + 0,6 c = 1,2 c
Das ist Überlichtgeschwindigkeit und damit eine resultierende Geschwindigkeit, die physikalisch nicht möglich ist. Offensichtlich muss für große Geschwindigkeiten ein anderes Gesetz gelten.

Addition von Geschwindigkeiten in der relativistischen Physik

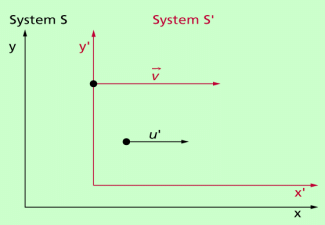
Wir betrachten nun ein analoges Beispiel, die Bewegung eines Massepunktes bei hohen Geschwindigkeiten: Ein Bezugssystem S' bewegt sich mit der Geschwindigkeit v gegenüber einem Bezugssystem S in positiver x-Richtung (Bild 2). Der Massepunkt bewegt sich bezüglich des Systems S' mit der Geschwindigkeit u' in der gleichen Richtung.

Mithilfe der LORENTZ-Transformation kann man eine Gleichung für die Geschwindigkeit des Massepunktes bezüglich des Systems S aus den Orts- und Zeitkoordinaten herleiten. Es gilt:
$\begin{array}{l}u=\frac{x_2-x_1}{t_2-t_1}=\frac{\Delta x}{\Delta t}\text{(1)}\\ \text{Für}\Delta x\text{erhält man mithilfe der Gleichungen für die}\\ \text{LORENTZ-Transformation:}\\ \Delta x=\frac{x_2\text{'}+v\cdot t_2\text{'}}{\sqrt{1-v^2/c^2}}-\frac{x_1\text{'}+v\cdot t_1\text{'}}{\sqrt{1-v^2/c^2}}\\ \Delta x=\frac{\Delta x\text{'}+v\cdot \Delta t\text{'}}{\sqrt{1-v^2/c^2}}\text{(2)}\\ \text{Für}\Delta t\text{erhält man mithilfe der Gleichungen für die}\\ \text{LORENTZ-Transformation in analoger Weise:}\\ \Delta t=\frac{\Delta t\text{'}+\frac{v}{c^2}\cdot \Delta x\text{'}}{\sqrt{1-v^2/c^2}}\text{(3)}\end{array}$

Setzt man die rechten Seiten der Gleichungen (2) und (3) in die Gleichung (1) ein, so erhält man:
$\begin{array}{l}u=\frac{\Delta x\text{'}+v\cdot \Delta t\text{'}}{\Delta t\text{'}+\frac{v}{c^2}\cdot \Delta x\text{'}}\\ \text{Dafür kann man auch schreiben:}\\ u=\frac{\frac{\Delta x\text{'}}{\Delta t\text{'}}+v}{1+\frac{v}{c^2}\cdot \frac{\Delta x\text{'}}{\Delta t\text{'}}}\\ \text{Mit}\frac{\Delta x\text{'}}{\Delta t\text{'}}=u\text{'}\text{erhält man:}\\ u=\frac{u\text{'}+v}{1+\frac{v\cdot u\text{'}}{c^2}}\end{array}$

Das bedeutet: Aus relativistischer Sicht addieren sich die Geschwindigkeiten nicht einfach, sondern es gilt für die relativistische Addition von Geschwindigkeiten die Gleichung:
$\begin{array}{l}u=\frac{u\text{'}+v}{1+\frac{u\text{'}\cdot v}{c^2}}\\ u\text{Geschwindigkeit bezüglich des Systems S}\\ u\text{'}\text{Geschwindigkeit bezüglich des Systems S'}\\ v\text{Relativgeschwindigkeit zwischen S und S'}\end{array}$

Betrachtung von Spezialfällen

Betragen die beiden Geschwindigkeiten u' und v jeweils c, dann erhält man:
$u=\frac{c+c}{1+\frac{c\cdot c}{c^2}}=\frac{2c}{2}=c$
Das steht in Übereinstimmung mit dem Postulat, dass die Vakuumlichtgeschwindigkeit die größtmögliche Geschwindigkeit ist.

Sind die Geschwindigkeiten u' und v klein gegenüber der Lichtgeschwindigkeit, dann geht der im Nenner stehende Term
$\frac{u\text{'}\cdot v}{c^2}$
gegen null. Die Gleichung geht damit in die für die Addition von Geschwindigkeiten in der klassischen Physik über. Bei den im Alltag üblichen Geschwindigkeiten kann man die Gleichung der klassischen Physik nutzen.

Beispiel: u' und v mögen jeweils einen Betrag von 1000 km/h haben. Dann hat der genannte Term einen Wert von etwa 0,000.000.3.

Experimentelle Bestätigung

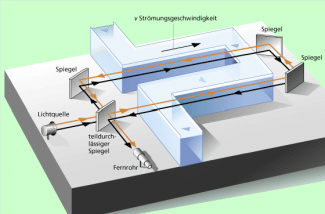
Eine experimentelle Bestätigung für die relativistische Addition von Geschwindigkeiten ergab ein Experiment, dass der französiche Physiker ARMAND-HIPPOLYTE-LOUIS FIZEAU 1851 durchgeführt hatte. Er maß mit einer speziell dafür geschaffenen Experimentieranordnung (Bild 3) die Lichtgeschwindigkeit in fließendem Wasser. Der teildurchlässige Spiegel teilt das Licht in einen Strahl, der in Strömungsrichtung verläuft (schwarz gezeichnet) und in einen Strahl, der entgegengesetzt der Strömungsrichtung läuft.
Das experimentelle Ergebnis entspricht dem, was man theoretisch bei Anwendung der relativistischen Addition von Geschwindigkeiten erhält. FIZEAU selbst wendete bei der Auswertung das klassische Gesetz an, musste aber einen nicht so recht erklärlichen Faktor einführen, um Theorie und Praxis in Übereinstimmung zu bringen.