Das Trägheitsgesetz (1. newtonsches Gesetz)
Das von GALILEO GALILEI (1564-1642) gefundene Trägheitsgesetz lautet:
Ein Körper bleibt in Ruhe oder in gleichförmiger geradliniger Bewegung, solange die Summe der auf ihn wirkenden Kräfte null ist.
ISAAC NEWTON (1643-1727) formulierte dieses Gesetz in klarer Form in Rahmen seiner newtonschen Mechanik. Es wird deshalb auch als 1. newtonsches Gesetz bezeichnet.
Aufgrund seiner Masse bleibt ein Körper in Ruhe, wenn die Summe der auf ihn wirkenden Kräfte null ist. Ein bewegter Körper, etwa ein fahrendes Auto oder ein Fahrgast in einem fahrenden Bus, versucht seinen Bewegungszustand beizubehalten. Die Eigenschaft von Körpern, aufgrund ihrer Masse ihren Bewegungszustand beizubehalten, wird als Trägheit bezeichnet. Abgeleitet ist dieser Begriff vom lateinischen inertia = Trägheit. Ein typisches Beispiel für die Trägheit von Körpern zeigt Bild 1. Im Unterschied zur Schwere, die immer an die Existenz weiterer Körper gebunden und untrennbar mit der Gravitation verbunden ist, tritt Trägheit überall als eine Eigenschaft massebehafteter Objekte auf. Das führt z.B. im Weltraum unter der Bedingung der Schwerelosigkeit dazu, dass sich ein einmal angestoßener Körper geradlinig und gleichförmig bewegt.
Die oben genannten Zusammenhänge zwischen dem Bewegungszustand eines Körpers und der auf ihn wirkenden Kräfte wurden erstmals von GALILEO GALILEI (1564-1642) systematisch untersucht und von ISAAC NEWTON (1643-1727) in Form eines seiner grundlegenden Axiome gebracht, die er 1687 in seinem fundamentalen Werk „Philosophiae naturalis principia mathematica“ (Mathematische Grundlagen der Naturwissenschaft) darstellte und die zu den Grundlagen der newtonschen Mechanik gehören.
Das Gesetz wird als 1. newtonsches Axiom, 1. newtonsches Gesetz oder Trägheitsgesetz bezeichnet und lautet:
Ein Körper bleibt in Ruhe oder in gleichförmiger geradliniger Bewegung, solange die Summe der auf ihn wirkenden Kräfte null ist.
Dieses Gesetz gilt in der genannten Form in allen unbeschleunigten Bezugssystemen, die man auch Inertialsysteme nennt. Und umgekehrt gilt: Ein Bezugssystem, in dem das Trägheitsgesetz gilt, wird als Inertialsystem bezeichnet. Nähere Erläuterungen dazu sind unter dem Stichwort „Bezugssysteme“ zu finden. Formal kann man das Trägheitsgesetz aus dem newtonschen Grundgesetz ableiten:
Aus historischen Gründen wird es aber zumeist als eigenständiges Gesetz betrachtet.
-
Wird beispielsweise ein Auto stark abgebremst, so bewegt sich der Fahrer - hier ein Dummy - aufgrund seiner Trägheit nach vorn.

3alexd - iStock by Getty Images
Beispiele für das Auftreten von Trägheit
Die Trägheit macht sich beim Beschleunigen oder beim Abbremsen von Körpern bemerkbar. Das kann man selbst feststellen, wenn man sich in einem Bus befindet. Beim Anfahren des Busses (Bild 2) fällt man aufgrund der Trägheit nach hinten, wenn man sich nicht festhält. Der Körper versucht, seinen ursprünglichen Bewegungszustand beizubehalten. Entsprechend gilt beim Bremsen (Bild 3), dass hier der Körper ebenfalls versucht, seinen Bewegungszustand beizubehalten und nach vorn fällt, wenn man sich nicht festhält.
Das kann man auch folgendermaßen interpretieren: In einem anfahrenden oder bremsenden Bus befindet man sich in einem beschleunigten Bezugssystem. In einem solchen Bezugssystem wirken aufgrund der Trägheit der Körper Trägheitskräfte, die man nach der Gleichung berechnen kann, wobei m die Masse des betreffenden Körpers und a seine Beschleunigung ist. Die Richtungen von Beschleunigung und Trägheitskraft sind immer entgegengesetzt gerichtet. Umfangreiche Informationen zu Trägheitskräften sind unter diesem Stichwort zu finden.
Auch bei Kurvenfahrten wirken Kräfte. In diesem Falle ändert sich die Richtung der Bewegung, wozu nach dem Trägheitsgesetz ebenfalls eine Kraft erforderlich ist. Befindet man sich z.B. in der Gondel eines Kettenkarussells und damit in einem beschleunigten Bezugssystem, so spürt man eine nach außen wirkende Kraft, die als Zentrifugalkraft bezeichnet wird. Auch die Zentrifugalkraft ist eine Trägheitskraft.
-
Trägheit beim Beschleunigen: Es wirkt eine Trägheitskraft entgegen der Richtung der Beschleunigung, also nach hinten.

H. Braun, Berlin
-
Trägheit beim Abbremsen: Es wirkt ebenfalls eine Trägheitskraft entgegen der Richtung der Beschleunigung, also nach vorn.
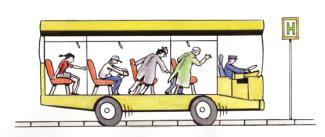
H. Braun, Berlin

