Das Wechselwirkungsgesetz (3. newtonsches Gesetz)
Wirken zwei Körper aufeinander ein, so wirkt auf jeden der Körper eine Kraft. Die Kräfte sind gleich groß und entgegengesetzt gerichtet:
Dieses Gesetz wurde von dem berühmten englischen Naturforscher ISAAC NEWTON (1643-1727) entdeckt. Es wird auch als 3. newtonsches Gesetz oder 3. newtonsches Axiom bezeichnet. Entsprechend seinem Inhalt spricht man auch vom Gegenwirkungsprinzip, von „actio = reactio“ oder von „Kraft = Gegenkraft“.
Das Wechselwirkungsgesetz gilt immer, wenn zwei Körper aufeinander einwirken. So zieht z.B. die Erde unseren Körper an, unser Körper zieht aber mit dem gleichen Betrag der Kraft auch die Erde an.
Bei einem Crashtest wirkt Auto 2 auf Auto 1, aber auch Auto 1 auf Auto 2 ein (Bild 1).
Beim Heben oder Tragen einer Tasche müssen wir eine Muskelkraft nach oben aufwenden. Die Gewichtskraft wirkt nach unten.
-
Die Kräfte sind gleich groß, aber entgegengesetzt gerichtet.

Wechselwirkung von Körpern und die dabei wirkenden Kräfte
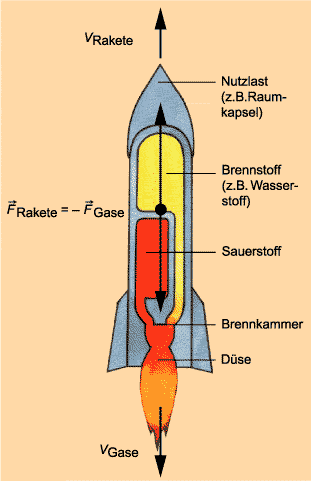
Das Wechselwirkungsgesetz ist auch der Grund dafür, dass sich eine Rakete oder ein Flugzeug fortbewegt (Bild 2). Aufgrund der starken Beschleunigung der Verbrennungsgase und ihrer Masse wirkt eine große Kraft entgegen der Bewegungsrichtung der Rakete. Nach dem Wechselwirkungsgesetz ist mit dieser Kraft eine gleich große,
aber entgegengesetzt wirkende Kraft verbunden. Diese Gegenkraft beschleunigt die Rakete in Bewegungsrichtung.
Eine bessere und eindeutigere physikalische Erklärung ist an dieser Stelle aber mithilfe von Impuls und Impulserhaltungssatz möglich.
-
Wechselwirkung bei einer Rakete
Sybille Storch, Berlin
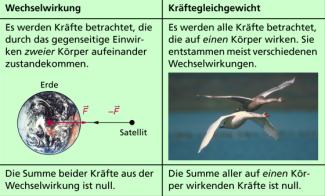
Wechselwirkung und Kräftegleichgewicht
Bei einer Wechselwirkung zwischen zwei Körpern treten zwei Kräfte auf, deren Summe null ist. Diese Kräfte kommen durch die gegenseitige Einwirkung der Körper aufeinander zustande. So zieht z.B. die Erde den Mond an. Der Mond zieht mit einer Kraft, die den gleichen Betrag hat, die Erde an (Bild 3). Die Betrachtungen beziehen sich also bei der Wechselwirkung immer auf mindestens zwei Körper, die sich gegenseitig beeinflussen.
Auch auf einen Körper kann die Summe der auf ihn wirkenden Kräfte null sein. Das gilt z.B. für ein gleichförmig und geradlinig fahrendes Auto, eine auf einem Tisch stehende Limonadenflasche oder einen Vogel (Bild 3). In diesem Falle, in dem man einen Körper und die auf ihn wirkenden Kräfte betrachtet, spricht man dann vom Kräftegleichgewicht, wenn sich alle auf den Körper wirkenden Kräfte gegenseitig aufheben und damit ihre Summe null ist.
-
Es muss klar zwischen einer Wechselwirkung und den damit verbundenen Kräften und einem Kräftegleichgewicht, in dem sich ein Körper befindet, unterschieden werden.
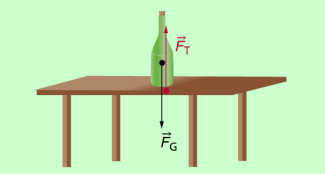
Die Kräfte, die auf einen Körper wirken, stammen meist aus verschiedenen Wechselwirkungen. Betrachtungen wir dazu den in Bild 4 dargestellten Fall, dass eine Flasche auf einem Tisch steht. Sie unterliegt folgenden Wechselwirkungen:
a) Wechselwirkung 1 zwischen Flasche und Erde: Die Erde zieht die Flasche mit der Gewichtskraft an, zugleich zieht die Flasche die Erde mit einer gleich großen Gegenkraft an.
b) Wechselwirkung 2 zwischen Flasche und Tisch: Die Flasche wirkt auf den Tisch ein und führt zu einer Verformung. Zugleich wirkt der Tisch mit einer gleich großen Gegenkraft auf die Flasche ein.
Betrachtet man nur die Kräfte, die auf die Flasche wirken, dann sind das aus Wechselwirkung 1 die Gewichtskraft und aus Wechselwirkung 2 die Kraft, die der Tisch auf die Flasche ausübt. Die Summe dieser beiden, aus verschiedenen Wechselwirkungen stammenden Kräfte ist null. Die Flasche befindet sich im Kräftegleichgewicht. Allgemein gilt:
Ein Körper befindet sich im Kräftegleichgewicht, wenn die Summe der auf ihn wirkenden Kräfte null ist.
-
Die beiden Kräfte, die auf die Flasche wirken, stammen aus verschiedenen Wechselwirkungen.