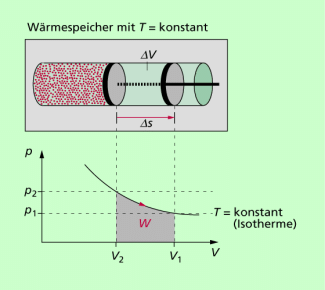
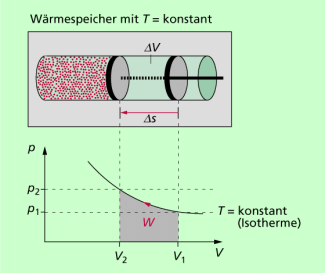
Isotherme Zustandsänderungen
Nach dem 1. Hauptsatz der Thermodynamik kann eine isotherme Zustandsänderung, also eine Zustandsänderung bei konstanter Temperatur, durch folgende Prozesse realisiert werden:
- Dem Gas wird eine Wärme Q zugeführt, es dehnt sich aus und verrichtet Volumenarbeit (isotherme Expansion).
- An dem Gas wird die äußere Arbeit W verrichtet, das Volumen wird kleiner und die dabei entstehende Wärme wird abgegeben (isotherme Kompression).
Die bei einer isothermen Expansion vom Gas verrichtete Arbeit (Volumenarbeit) entspricht der Fläche unterhalb der Isobare im p-V- Diagramm. Sie kann durch Auszählen der Fläche oder durch Integration berechnet werden. Bei Verwendung des Modells ideales Gas beträgt die Volumenarbeit bei isothermer Expansion:
Diese Arbeit ist gleich der dem Gas zugeführten Wärme, die dieses benötigt, um seine innere Energie bei der Expansion konstant zu halten.
Zustandsänderungen von Gasen sind im allgemeinen komplizierte, komplexe Vorgänge. Zur Vereinfachung werden darum thermodynamische Prozesse oft in Teilprozesse zerlegt, bei denen eine oder auch mehrere Zustandsgrößen als konstant angenommen werden. Beispiele dafür sind die in Verbrennungsmotoren, Dampfmaschinen oder STIRLING-Motoren ablaufenden Kreisprozesse. Erst durch die Zerlegung in einzelne „Arbeitstakte“ lässt sich die Funktionsweise der Energiewandler mithilfe von thermodynamischen Gesetzen erklären. Von einer isothermen Zustandsänderung spricht man, wenn diese bei konstanter Temperatur vor sich geht. Im Allgemeinen ändern sich dann Druck und Volumen des Gases.
Isotherme Expansion und Kompression
Nach dem 1. Hauptsatz der Thermodynamik wird eine Änderung der inneren Energie eines Gases durch Zuführung einer Wärme Q oder durch Verrichten von äußerer Arbeit W erreicht.
Bei isothermen Zustandsänderungen bleibt die Temperatur des Gases konstant, d.h. die innere Energie des Gases ändert sich nicht.
Das lässt sich durch folgende Prozesse realisieren:
| |
| |
Berechnung der Volumenarbeit
Die bei einer isothermen Expansion vom Gas verrichtete Arbeit (Volumenarbeit) kann berechnet werden mit der Gleichung:
Sie entspricht der Fläche unterhalb des Graphen (Isotherme) im p-V-Diagramm (Bild 1). Sie ist umso größer, je höher die Temperatur ist und je größer die Volumenänderung ist.
Die bei der isothermen Kompression von bei gleicher Temperatur aufzuwendende Arbeit ist betragsmäßig genau so groß wie die verrichtete Arbeit bei der isothermen Expansion.
Bei Verwendung des Modells ideales Gas kann die Volumenarbeit bei isothermer Expansion folgendermaßen ermittelt werden:
Die Zustandsgleichung des idealen Gases
reduziert sich für isotherme Prozesse auf
und damit die Beziehung zwischen dem Anfangs- und dem Endzustand der Zustandsänderung auf .
Für die Untersuchung der Druck- und Volumenänderung eines Gases bei Zuführung von Wärme sind diese Annahmen für viele praktische Prozesse durchaus gerechtfertigt.
Nach Einsetzen der Zustandsgleichung in die Gleichung für die Volumenarbeit ergibt sich die vom Gas geleistete Volumenarbeit bei isothermer Expansion durch Integration:
Wird die Zustandsgleichung des idealen Gases benutzt, so kann die Volumenarbeit auch in der Form
geschrieben werden. Durch die Einführung der Masse m des Gases und der spezifischen Gaskonstanten ![]() kann mithilfe der Beziehungen
kann mithilfe der Beziehungen
die Volumenarbeit bei isothermer Expansion umgeformt werden in:
Diese Arbeit ist gleich der dem Gas zugeführten Wärme, die dieses benötigt, um seine innere Energie bei der Expansion konstant zu halten.