Kräfte und ihre Messung
Der Begriff Kraft wird im Alltag und in der Physik in vielfältiger Weise verwendet. Während der Alltagsbegriff mit unterschiedlichen Begriffsinhalten genutzt wird, ist die physikalische Größe Kraft eindeutig definiert:
Die Kraft gibt an, wie stark ein Körper bewegt oder verformt wird. Sie ist eine Wechselwirkungsgröße und eine vektorielle (gerichtete) Größe. Die Wirkung einer Kraft ist abhängig von ihrem Betrag, ihrer Richtung und ihrem Angriffspunkt.
Man unterscheidet u.a. elektrische Kräfte, magnetische Kräfte, Reibungskräfte, Druckkräfte, Radialkräfte, Gewichtskräfte, Schubkräfte, Spannkräfte und Zugkräfte, Adhäsionskräfte und Kohäsionskräfte, innere Kräfte und äußere Kräfte voneinander.
Kräfte und ihre Messung
Die physikalische Größe Kraft
Der Begriff Kraft wird im Alltag und in der Physik in vielfältiger Weise verwendet. Während der Alltagsbegriff mit unterschiedlichen Begriffsinhalten genutzt wird, ist die physikalische Größe Kraft eindeutig definiert:
Die Kraft gibt an, wie stark ein Körper bewegt oder verformt wird. Sie ist eine Wechselwirkungsgröße und eine vektorielle Größe.
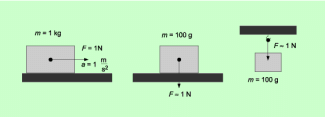
Ein Newton (1 N) ist die Kraft, die einem Körper der Masse 1 kg eine Beschleunigung von erteilt. Es ist etwa die Kraft, mit der ein Körper der Masse 100 g auf eine ruhende Unterlage drückt oder an einer Aufhängung zieht (Bild 2). Benannt ist diese Einheit nach dem berühmten englischen Physiker ISAAC NEWTON (1643-1727). Weitere übliche Einheiten sind die Vielfachen
1 kN = 1000 N und
1 MN = 1000 kN = 1000000 N
sowie der Teil
1 mN = 0,001 N.
Nicht mehr verwendet werden die früher üblichen Einheiten Kilopond (kp) und Dyn (dyn).
Darstellung von Kräften
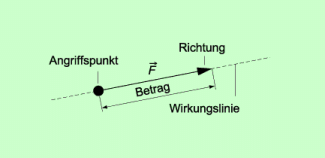
Als vektorielle Größe wird eine Kraft als Pfeil dargestellt (Bild 3). Sie ist gekennzeichnet durch den Betrag (Länge des Pfeils), die Richtung (Pfeilspitze) und den Angriffspunkt . Dabei sind folgende Besonderheiten zu beachten:
- Will man Kräfte ihrem Betrag entsprechend darstellen, so muss vorher ein Maßstab vereinbart werden.
- Statt von Richtung spricht man manchmal auch von Richtungssinn. Die Sprachregelung ist Sache der Vereinbarung. Wir verwenden den Begriff Richtung und meinen bei Kräften die durch die Pfeilspitze angegebene Orientierung, die man auch mit dem Terminus „Richtungsssinn“ bezeichnet.
- Kräfte sind „linienflüchtige“ Vektoren, d.h. an der Wirkung einer Kraft ändert sich nichts, wenn sie entlang der Wirkungslinie verschoben wird.
Wirkungen von Kräften
Eine Kraft ist nur an ihren Wirkungen erkennbar. Die Wirkung einer Kraft auf einen Körper ist abhängig von ihrem Betrag, ihrer Richtung und ihrem Angriffspunkt. Kräfte können Bewegungsänderungen und Formänderungen bei Körpern hervorrufen, die im Extremfall bis zur Zerstörung des Körpers führen können.
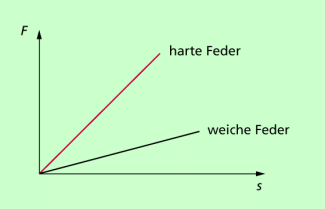
Die Formänderungen können dabei elastisch oder plastisch erfolgen. Eine elastische Verformung liegt vor, wenn ein Körper nach der Krafteinwirkung von allein wieder seine ursprüngliche Form annimmt, so wie das z.B. bei Stahlfedern der Fall ist. Zwischen der wirkenden Kraft und der Ausdehnung besteht in diesem Falle direkte Proportionalität (Bild 4). Bereits der englische Naturforscher ROBERT HOOKE (1635-1703) fand heraus, dass für eine elastische Verformung gilt:
Dieser Zusammenhang, der unter der Bedingung einer elastischen Verformung gilt, wird als hookesches Gesetz bezeichnet.
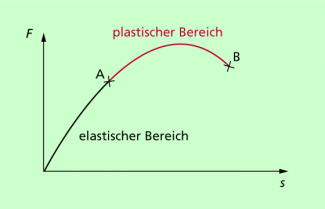
Eine plastische Verformung liegt dagegen vor, wenn ein Körper nach der Krafteinwirkung nicht von allein wieder seine ursprüngliche Form annimmt. Solche plastischen Verformungen treten z.B. beim Schmieden oder in der Verformungstechnik auf. Eine plastische Verformung erfolgt auch, wenn beispielsweise ein Stahldraht über seine Elastizitätsgrenze hinaus belastet wird (Bild 5). Bis zum Punkt A erfolgt eine elastische Verformung. Es gilt das hookesche Gesetz. Bei A wird die Elastizitätsgrenze erreicht. Die weitere Verformung erfolgt plastisch, wobei bei B die Bruchgrenze erreicht wird, der Draht also reißt.
Messen von Kräften
Unterschieden wird zwischen der statischen und der dynamischen Kraftmessung. Beide Arten werden nachfolgend charakterisiert.
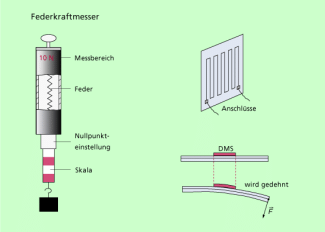
Statische Kraftmessung : Die Messung der Kraft erfolgt bei ruhendem Körper. Als Messgeräte kann man z.B. Federkraftmesser oder Dehnungsmessstreifen (DMS) verwenden (Bild 6). Beim Federkraftmesser wird das hookesche Gesetz genutzt. Dabei ist zu beachten, dass die Feder eines Federkraftmessers nicht überdehnt werden darf.
Dehnungsmessstreifen (DMS) bestehen meist aus dünnem Widerstandsdraht oder Widerstandsfolie, die auf einen verformbaren Träger aufgebracht sind (Bild 6). Ändert sich durch Biegung die Länge oder die Dicke des DMS, so verändert sich auch sein elektrischer Widerstand und damit die Stromstärke durch den DMS. Die Stromstärke ist damit ein Maß für die einwirkende Kraft. Die entsprechenden Messgeräte sind so geeicht, dass in der Regel eine digitale Anzeige der Kraft erfolgt.
Dynamische Kraftmessung : Die Kraft kann auch unter Nutzung des newtonsches Grundgesetzes gemessen werden. Kennt man die Masse des Körpers und bestimmt seine Beschleunigung, so kann man daraus die auf ihn einwirkende Kraft bestimmen.
Berechnen von Kräften
Die in der Physik auftretenden Kräfte sind außerordentlich vielfältig. Darüber hinaus gibt es aufgrund dieser Vielfalt keine eindeutige Systematisierung. Wir beschränken uns daher nachfolgend auf ausgewählte Beispiele.
Allgemein gilt das newtonsche Grundgesetz in der Form
Diese Gleichung lässt sich auch auf viele spezielle Fälle anwenden. Einige von ihnen sind in der nachfolgenden Tabelle erfasst.
| Art der Kraft | Berechnungs- | Bedeutung der Größen |
| allgemein | m Masse des Körpers a Beschleunigung des Körpers | |
| Gewichtskraft | m Masse des Körpers g Fallbeschleunigung (Ortsfaktor) | |
| Reibungskraft | ||
| Federspannkraft | D Federkonstante s Längenänderung der Feder | |
| Radialkraft (Zentralkraft) | m Masse des Körpers v Geschwindigkeit des Körpers r Radius der Kreisbahn | |
| Auftriebskraft | ||
| Gravitationskraft |
Arten von Kräften
Es gibt viele verschiedene Arten von Kräften , die man z. B. nach der Art ihrer Entstehung oder nach der Art ihres Wirkens einteilen kann, wobei es allerdings keine eindeutige und alle Kräfte umfassende Systematisierung gibt. Wir stellen deshalb nachfolgend nur einige ausgewählte Arten dar. Diese verschiedenen Arten von Kräften sind in der Regel unter den betreffenden Stichwörtern ausführlich auf der CD dargestellt.
Kräfte zwischen geladenen Teilchen oder Körpern werden als elektrische Kräfte bezeichnet, solche zwischen Magneten oder zwischen Magneten und Körpern als magnetische Kräfte, solche zwischen Körpern als Gravitationskräfte. Physikalischer Hintergrund ist hier stets die Kraft, die auf Körper in einem Feld (elektrisches Feld, magnetisches Feld, Gravitationsfeld) wirkt. Man spricht deshalb auch von einer Feldkraft. Solche Feldkräfte wirken auch, wenn sich geladenen Teilchen, z.B. Elektronen, in elektrischen oder magnetischen Feldern bewegen.
Im Bereich der Mechanik wird z.B. unterschieden zwischen Gewichtskräften, Reibungskräften, Druckkräften, Federkräften oder Auftriebskräften, also nach der Art des Zustandekommens. Bei Kräften bei der Kreisbewegung gibt es die Radialkraft (Zentripetalkraft) und die Zentrifugalkraft und damit eine Unterscheidung in Abhängigkeit von dem Bezugssystem, von dem aus man die Bewegung beschreibt.
Zwischenmolekulare Kräfte werden als Kohäsionskräfte bzw. als Adhäsionskräfte bezeichnet. Im atomaren Bereich spielt die Kernkraft eine entscheidende Rolle.
Betrachtet man physikalische Systeme, so ist manchmal eine Unterscheidung zwischen inneren Kräften und äußeren Kräften zweckmäßig. Innere Kräfte sind solche, die innerhalb der Systemgrenze zwischen den Körpern oder Teilchen wirken, die zum System gehören. Äußere Kräfte greifen „von außen“ am System an.
In beschleunigten Bezugssystemen spielen Scheinkräfte oder Trägheitskräfte eine wichtige Rolle, z.B. die CORIOLIS-Kraft für die atmosphärischen Luftbewegungen, die Zentrifugalkraft bei Zentrifugen oder rotierenden Maschinenteilen oder die Trägheitskräfte, die man in anfahrenden oder bremsenden Fahrzeugen spürt.
Allein diese kurze und keineswegs vollständige Aufzählung zeigt, wie außerordentlich vielfältig der Kraftbegriff in der Physik verwendet wird und welche zentrale Rolle er an vielen Stellen spielt. Dabei ist auch zu beachten, dass die Begriffsvielfalt sehr groß und die Terminologie mitunter unterschiedlich ist.
Suche nach passenden Schlagwörtern
- interaktive Experimente
- statische Kraftmessung
- Wechselwirkungsgröße
- Arten von Kräften
- zwischenmolekulare Kräfte
- Berechnung
- Richtung
- Federspannkraft
- magnetische Kräfte
- Adhäsionskraft
- Betrag
- Elastische Verformung
- Dehnungsmessstreifen
- Gravitationskräfte
- Reibungskraft
- Druckkraft
- gerichtete Größe
- Bewegungsänderungen
- Kohäsionskraft
- innere Kraft
- Auftriebskraft
- Plastische Verformung
- Zentralkraft
- vektorielle Größe
- äußere Kraft
- Trägheitskräfte
- dynamische Kraftmessung
- ROBERT HOOKE
- Federkraftmesser
- DMS
- Isaac Newton
- Formänderungen
- Kohäsionskräfte
- Gewichtskraft
- Gravitationskraft
- Angriffspunkt
- Radialkraft
- Trägheitskraft
- Kraft
- Simulation
- Kräfte
- Rechenbeispiel
- Adhäsionskräfte
- Feldkraft
- elektrische Kräfte
- Wirkungslinie
- hookesches Gesetz
- Richtungssinn