Kurvenfahrten

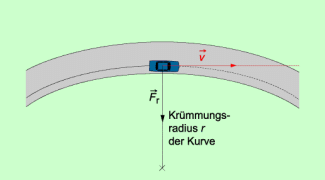
Zum sicheren Durchfahren einer Kurve muss bei jedem Fahrzeug eine Kraft in Richtung Zentrum der Kreisbewegung wirken. Diese radial gerichtete Kraft, die Radialkraft, wird durch die Reibung zwischen Straße und Reifen aufgebracht.
Die aufzubringende Radialkraft ist umso größer,

• je größer die Geschwindigkeit des Fahrzeuges ist,
• je größer seine Masse ist,
• je kleiner der Krümmungsradius der Kurve ist.

Für die erforderliche Radialkraft gilt die Gleichung:

$F_r=m\cdot \frac{v^2}{r}$

Kann z. B. durch eine zu geringe Reibung die für eine Kurvenfahrt erforderliche Radialkraft nicht mehr aufgebracht werden, so bewegt sich das Fahrzeug in tangentialer Richtung (Bild 2).

Berechnung der maximal möglichen Geschwindigkeit
Geht man davon aus, dass bei ebener Straße die erforderliche Radialkraft$F_r$durch die Reibungskraft $F_R$aufgebracht wird, dann gilt für die maximale Geschwindigkeit:

$F_r=F_R$

Setzt man für beide Kräfte ein, so erhält man:

$m\cdot \frac{v^2}{r}=\mu \cdot m\cdot g$

Die Umformung nach der Geschwindigkeit v ergibt:

$\begin{array}{l}v=\sqrt{\mu \cdot r\cdot g}\\ \mu \text{ Reibungszahl }\\ r\text{ Radius der Kreisbahn}\\ \text{ (Krümmungsradius der Kurve)}\\ g\text{ Fallbeschleunigung}\end{array}$

Das bedeutet: Die maximal mögliche Geschwindigkeit beim Durchfahren einer Kurve hängt nur vom Krümmungsradius der Kurve und von der Reibungszahl ab. Die Masse des Fahrzeuges spielt keine Rolle, weil sich die Radialkraft und die Reibungskraft in gleicher Weise mit Veränderung der Masse ändern.

Kurvenfahrten bei Autos und Schienenfahrzeugen
Im Unterschied zu Zweiradfahrzeugen erfolgt bei diesen Fahrzeugen bei Kurvenfahrten keine Neigung der Fahrzeuge selbst, wenn man von dem speziellen Fall von Neigezügen absieht. An vielen Stellen werden deshalb Kurven überhöht, um ein sicheres Durchfahren zu gewährleisten.
Wir betrachten nachfolgend zwei unterschiedliche Fälle.

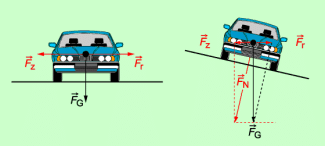
Bei Kurven ohne Überhöhung wirkt auf das Fahrzeug die Gewichtskraft und eine nach außen gerichtete Kraft, die Zentrifugalkraft. Sie wird kompensiert durch eine nach innen wirkende Kraft, die durch die Reibung zwischen Reifen und Fahrbahn aufgebracht wird.

Bei Kurven mit Überhöhung wirken ebenfalls die genannten Kräfte. Die Überhöhung ist so ausgelegt, dass bei der maximal zulässigen Geschwindigkeit die eine Komponente der Gewichtskraft senkrecht auf der Fahrbahnebene steht und somit als Normalkraft wirkt. Die andere Komponente der Gewichtskraft ist die Radialkraft, die durch die Zentrifugalkraft kompensiert wird (Bild 3).

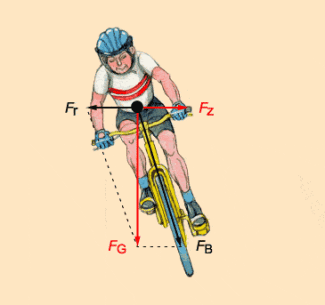
Kurvenfahrten bei Zweirädern
Bild 4 zeigt die bei einem Radfahrer wirkenden Kräfte bei nicht überhöhter Kurve. Es wirken die Gewichtskraft und die Zentrifugalkraft. Die schwarz eingezeichneten Kräfte sind Komponenten der Gewichtskraft. Die Radialkraft ist in diesem Fall also eine Komponente der Gewichtskraft.