Standfestigkeit von Körpern
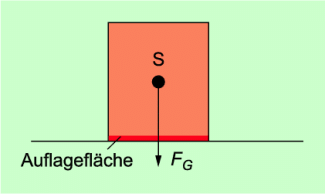
Gebäude, Türme, Krane oder Regale sollen standfest sein, also nicht umkippen. Entscheidend für die Standfestigkeit eines Körpers ist die Lage seines Schwerpunktes bezüglich seiner Auflagefläche. Ein Körper ist dann standfest, wenn die am Schwerpunkt angreifende Gewichtskraft durch die Auflagefläche verläuft. Der Körper befindet sich stets im stabilen Gleichgewicht.
Wird er aus seiner stabilen Lage gebracht, dann wirkt auf ihn ein Drehmoment in der Weise, dass er wieder in die stabile Lage kommt.
-
Ein standfester Körper: Die Gewichtskraft verläuft durch die Auflagefläche.
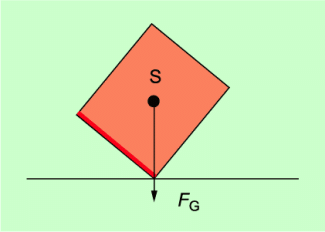
Ein kritischer Punkt bezüglich Standfestigkeit ist genau dann erreicht, wenn die am Schwerpunkt angreifende Gewichtskraft durch den Rand der Auflagefläche verläuft (Bild 2). Der Körper befindet sich dann in einem labilen Gleichgewicht. Eine geringfügige Veränderung der Lage führt dazu, dass der Körper entweder wieder in eine stabile Lage kommt oder umkippt und damit eine neue stabile Lage erreicht..
-
Ein kritischer Punkt bezüglich Standfestigkeit: Der Körper ist labil.
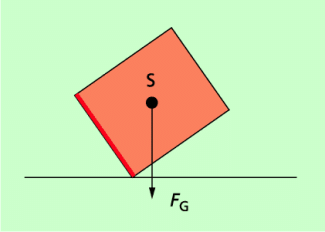
Verläuft die am Schwerpunkt des Körpers angreifende Gewichtskraft nicht durch die Auflagefläche, so kippt der Körper auf jeden Fall um, wenn er sich selbst überlassen bleibt. Er gelangt danach in eine neue, in der Regel stabile Lage mit einer anderen Auflagefläche.
Alle oben genannten Betrachtungen zur Standfestigkeit gelten für massive Körper. Zusätzliche und teilweise sehr komplizierte Überlegungen sind dann erforderlich, wenn ein Körper aus einzelnen Teilen (Ziegeln, Platten, Streben, Säulen) besteht, die alle die Stabilität des gesamten Körpers beeinflussen. Das gilt z.B. für nicht senkrecht stehende Bauwerke wie den schiefen Turm von Pisa, der inzwischen wieder etwas aufgerichtet und damit stabilisiert wurde.
-
Der Körper ist nicht standfest. Wenn nicht zusätzliche Kräftre wirken, kippt er um und befindet sich dann wieder in einem stabilen Gleichgewicht.