Grundgesetz der Dynamik der Rotation

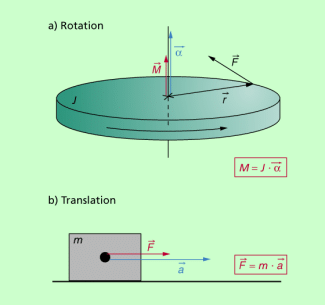
Für die Rotation starrer Körper gibt es ein analoges Gesetz, das Grundgesetz der Dynamik der Rotation. Zu diesem Gesetz gelangt man auf formalem Wege, wenn man in das newtonsche Grundgesetz für die Größen der Translation die analogen Größen der Rotation einsetzt. Man erhält dann eine Gleichung, die als Grundgesetz der Dynamik der Rotation bezeichnet wird (Bild 1). Sie gibt den Zusammenhang zwischen dem auf einen drehbaren starren Körper wirkenden Drehmoment, seinem Trägheitsmoment und der Winkelbeschleunigung an und lautet:

Für den Zusammenhang zwischen dem an einem Körper angreifenden Drehmoment, seinem Trägheitsmoment und der Winkelbeschleunigung gilt die Gleichung:
$\begin{array}{l}\overrightarrow{M}=J\cdot \overrightarrow{\alpha }\\ M\text{Drehmoment}\\ J\text{Trägheitsmoment}\\ \alpha \text{Winkelbeschleunigung}\end{array}$

Das Drehmoment $M=r\cdot F$ ist ein axialer Vektor (Bild 1a) und hat die gleiche Richtung wie die Winkelbeschleunigung, die es hervorruft. Die Richtung ergibt sich durch Anwendung der Rechte-Hand-Regel (Korkenzieherregel): Zeigen die gekrümmten Finger der rechten Hand in Drehrichtung, so gibt der Daumen die Richtung des Drehmomentes und damit auch die Richtung der Winkelbeschleunigung an.

Gleichgewicht am starren Körper

Bei der Translation befindet sich ein Massepunkt dann im Gleichgewicht (Kräftegleichgewicht), wenn die Summe der auf ihn wirkenden Kräfte null ist.
Formal bedeutet das:
$\begin{array}{l}\text{Für}F=0\text{bzw}\text{.}{\displaystyle \sum _{\text{i=1}}^{\text{n}}{\overrightarrow{F}}_i=\overrightarrow{0}\text{ist auch die Beschleunigung}}\\ a=0.\text{Der Körper befindet sich in Ruhe oder in}\\ \text{gleichförmiger geradliniger Bewegung}\text{.}\end{array}$

In analoger Weise ergibt sich für einen drehbar gelagerten starren Körper:
$\begin{array}{l}\text{Für}M=0\text{bzw}\text{.}{\displaystyle \sum _{\text{i=1}}^{\text{n}}{\overrightarrow{M}}_i=\overrightarrow{0}\text{ist auch die Winkelbeschleunigung}}\\ \alpha =0.\text{Der Körper befindet sich in Ruhe oder in}\\ \text{gleichförmiger Drehbewegung}\text{.}\end{array}$