Fahrphysik
Das Fahrverhalten von Kraftfahrzeugen wird im Wesentlichen durch die Konstruktion (z. B. Vorder-, Hinter- bzw. Allradantrieb, Fahrzeugart, Radstand, Spurweite, Achsbelastung) und das Wirken von äußeren Kräften bestimmt und wird bei besonderen Fahrsituationen (z.B. Anfahren, Bremsen, Kurvenfahrten) deutlich. Dargestellt und an Beispielen erläutert sind die unterschiedlichen Fahrzeugbewegungen, die verschiedenen Arten von Reibung, das Beschleunigen, Bremsen, Kurvenfahrten und Achsbelastungen.
Karosserie und Fahrzeugbewegung
Die wichtigsten Bewegungen eines Fahrzeuges sind das Stampfen, das Wippen, das Wanken und das Gieren (vgl. Bild 1). Diese Begriffe wurden der Seefahrt entlehnt.
Stampfen: Vertikale, geradlinige Schwingung längs der z-Achse, also das wechselseitige Steigen und Sinken der Karosserie in der Federung.
Wippen (Nicken): Rotationsbewegungen um die y-Achse, die zum Beispiel beim Bremsen oder Beschleunigen als Folge der dynamischen Achslastverschiebungen entstehen, aber auch beim Fahren über Unebenheiten.
Wanken (Rollen): Rotationsbewegungen um die x-Achse
Diese Karosseriebewegung tritt als Neigen nach außen in der Kurve, aber auch bei Windböen auf.
Gieren: Rotationsbewegungen um die z-Achse bei Kurvenfahrten.
Im Wesentlichen wird beim Stampfen durch die Wellenlänge der Straßenunebenheiten und die Fahrzeuggeschwindigkeit v der Federung eine Frequenz aufgezwungen:
Bedeutsame Wellenlängen sind bei einer Betonautobahn 10 m bis 15 m, bei einer Klinkerstraße 1 m bis 2 m und bei einer Straße mit Katzenkopfpflasterung 0,1 m bis 0,25 m.
Dadurch kann es beim Fahren über diese Straßenoberflächen zu Resonanzerscheinungen kommen, wenn diese Frequenz mit Eigenfrequenzen einzelner Fahrzeugteile übereinstimmt. Typische Eigenfrequenzen sind bei Lenkradschwingungen 25 Hz bis 40 Hz, für das Dröhnen im Fahrgastraum 30 Hz bis 200 Hz und bei einem sehr weichen Federsystem 0,1 Hz bis 0,5 Hz.
Bei den Rotationsbewegungen (Wanken, Wippen, Gieren) sind die Größen der jeweiligen Trägheitsmomente bedeutsam:
- Für Untersuchungen der Fahrstabilität oder zur Rekonstruktionen von Verkehrsunfällen wird das Trägheitsmoment des Gesamtfahrzeuges um die z-Achse benötigt:
Das Fahrverhalten in Kurven wird mit abnehmendem Trägheitsmoment besser, im gleichen Maße verschlechtert sich die Fahrstabilität bei Geradeausfahrt oder bei Wechselkurven (z. B. beim Ausweichen von Hindernissen). - Bei Untersuchungen der Wankbewegungen der Karosserie während schneller Fahrtrichtungsänderungen ist ihr Trägheitsmoment um die x-Achse maßgebend:
(Gefahr des Umkippens - dem soll unter anderem das elektronische Stabilisierungsprogramm ESP entgegenwirken). - Zur Ermittlung des Nickschwingungsverhaltens, z. B. beim Anfahren, Beschleunigen und Bremsen, stellt das Trägheitsmoment der Karosserie um die y-Achse die entscheidende Größe dar:
Für eine Mittelklasselimousine (Masse des Fahrzeugs 900 kg, Masse der Karosserie 700 kg) ergeben sich folgende Werte für die Trägheitsradien:
| Zuladung | Trägheitsradien in m | ||
| keine | 1,20 | 0,65 | 1,21 |
| 2 Personen | 1,15 | 0,64 | 1,13 |
| 4 Personen | 1,14 | 0,60 | 1,10 |
| 4 Personen und Gepäck | 1,18 | 0,56 | 1,13 |
-
Bewegungen eines Pkw um verschiedene Achsen

Kräfte längs der Fahrtrichtung
Die wesentlichen Kräfte, die beim Fahren mit konstanter Geschwindigkeit überwunden werden müssen, sind die Rollreibungskraft und die Luftwiderstandskraft. Die zwischen Reifen und Straßenbelag auftretende Haftreibung ermöglicht erst die Änderung der Geschwindigkeit und der Fahrtrichtung.
Rollreibung
Durch das Abrollen des Rades auf der Fahrbahn erfolgt sowohl eine Verformung des Rades als auch der Fahrbahn (an den Spurrinnen erkennbar). Zusätzlich treten auch Reibungskräfte im Fahrzeug (z.B. Achslagerung) auf. Die Rollreibungskraft kann vereinfacht berechnet werden durch:
Die Rollreibungszahl (auch Fahrwiderstandszahl oder Rollwiderstandskoeffizient genannt) hängt ab von
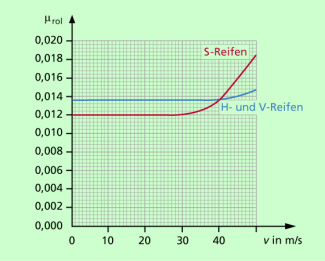
| - | der Fahrzeuggeschwindigkeit (Bild 2), | ||
| - | der Reifenart (Bild 2), dem Reifendruck und der Reifentemperatur, | ||
| - | der Beschaffenheit der Straßenoberfläche (s. Tabelle unten). | ||
| S - Reifen | Diese Reifenart ist bis zu einer Geschwindigkeit von 180 km/h zugelassen. Ihre Gummimischung wurde so gewählt, dass die Rollreibung möglichst gering ausfällt, um den Kraftstoffverbrauch und damit die Betriebskosten gering zu halten. | ||
| H - und V - Reifen | Diese Reifenarten sind für Geschwindigkeiten bis 210 km/h (H) bzw. 240 km/h(V) zugelassen. Die Zusammensetzung des Gummis wurde so gewählt, dass durch eine höhere Haftreibung (und damit auch ein höherer Rollreibung) eine größere Sicherheit insbesondere auf nasser Fahrbahn gewährleistet ist. | ||
Die nachfolgende Übersicht zeigt Werte für die Rollreibungszahl für S-Reifen und Geschwindigkeiten unter 100 km/h.
| Straßenbelag | Rollreibungszahl |
| Asphalt | 0,015 |
| rauer Beton | 0,017 |
| unbefestigte Straße | 0,3 |
Bei einer Kurvenfahrt nimmt durch die zusätzliche Verformung des Reifens die Rollreibung stark zu (bis zu 60 % bei Querbeschleunigungen von ).
Für den Zusammenhang von Rollreibung und Kraftstoffverbrauch kann folgende Faustregel angewendet werden: Eine Absenkung der Rollreibungszahl um 6% führt zu einer Kraftstoffeinsparung um 1%.
-
Abhängigkeit der Rollreibungszahl von der gefahrenen Geschwindigkeit für verschiedene Arten von Reifen. Die Messung erfolgte auf einem Trommelprüfstand.
Luftwiderstand
Die beim Fahren aufzubringende Kraft zur Überwindung des Luftwiderstands kann mit folgender Formel berechnet werden:
Dabei sind die Dichte der Luft bei 15 °C und einem Luftdruck von 1013 hPa, A die frontale Querschnittsfläche des Autos (meist zwischen 1,6 Quadratmeter und 2,5 Quadratmeter), die durch die Bauform bedingte Luftwiderstandszahl (Bild 3) und v die gefahrene Geschwindigkeit.
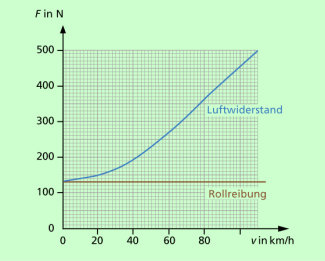
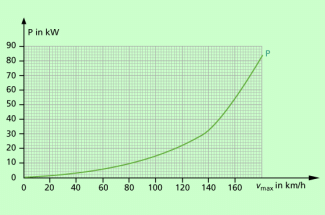
Bei Geschwindigkeiten unter 25 km/h spielt der Luftwiderstand nur eine geringe Rolle (Bild 4). Er ist aber wesentlich für die Begrenzung der Höchstgeschwindigkeit verantwortlich (Bild 5).
Die Höchstgeschwindigkeit kann vereinfacht aus der Motorleistung mithilfe der folgenden Gleichung bestimmt werden:
Damit wird die gesamte Motorleistung zum Aufrechterhalten einer konstanten Geschwindigkeit auf einer ebenen Straße eingesetzt. Ein Beschleunigen oder Berganfahren ist dann nicht mehr möglich.
-
Abhängigkeit der Luftwiderstandszahl von der Bauform

-
Rollreibungskraft und Luftwiderstandskraft in Abhängigkeit von der Geschwindigkeit für einen Pkw der Mittelklasse auf der Autobahn,
-
Zusammenhang zwischen der Motorleistung eines Mittelklasse-Pkw und der erreichbaren Höchstgeschwindigkeit auf der Autobahn.
Haftreibung
Die Deformierung der Reifen erfordert einerseits Arbeit (Rollreibung), ermöglicht aber andererseits erst die Kraftübertragung zwischen Fahrzeug und Fahrbahn beim Anfahren, Beschleunigen, Bremsen und in der Kurvenfahrt. Durch diese Deformierung verursachen Teile der Lauffläche, während sie unter Last abrollt, eine Relativbewegung zwischen Lauffläche und Fahrbahn. Damit entspricht die Umfangsgeschwindigkeit des Reifens nicht mehr der Fahrzeuggeschwindigkeit. Daraus kann das Längsgleiten, eine für die Beschreibung des Fahrverhaltens charakteristische Größe, bestimmt werden:
Zwischen der wirksamen Reibungszahl und dem Längsgleiten wurde der in Bild 6 dargestellte Zusammenhang ermittelt. Für die wirksame Reibungszahl gilt:
-
Änderung der Reibungszahl bei unterschiedlichem Längsgleiten
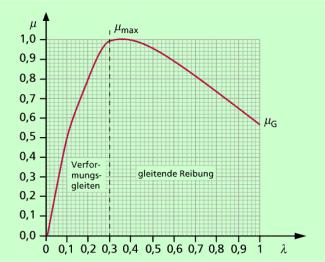
Zur maximalen Kraftübertragung beim Beschleunigen und Bremsen ist also immer eine geeignete Drehzahl der Räder notwendig.
In der Praxis ist die maximale Reibungszahl gleich der Haftreibungszahl. Diejenige Reibungszahl, die ermittelt wurde, wenn das Rad blockiert über die Fahrbahn gleitet, wird Gleitreibungszahl genannt.
In der nachfolgenden Übersicht ist die maximale Reibungszahl für einen Pkw mit S-Reifen (90 % Profil) bei einer Geschwindigkeit von 60 km/h angegeben.
| Straßenoberfläche | Haftreibungszahl |
| Asphalt trocken | 1,10 |
| Asphalt nass | 0,85 |
| loser Kies | 0,50 |
| Schnee | 0,20 |
| Glatteis | 0,10 |
| Schneematsch bei 0 °C | 0,06 |
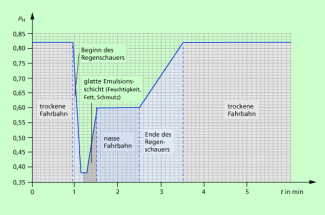
Bild 7 zeigt, wie sich die Haftreibungszahl bei einem Regenschauer ändert.
-
Veränderung der Haftreibungszahl zwischen Reifen und Fahrbahn während eines Regenschauers bei unterschiedlichen Bedingungen:I trockene FahrbahnII Beginn des Regenschauers mit zunehmender Feuchtigkeit auf der FahrbahnIII Schicht aus Feuchtigkeit, Fett und Schmutz, die allmählich abgewaschen wirdIV nasse FahrbahnV Ende des Regenschauers und Abtrocknen der FahrbahnVI trockene Fahrbahn
Beschleunigen, Bremsen und Kurvenfahrt
Wesentlichen Einfluss auf das Fahrverhalten eines Pkw hat die Achsbelastung. Diese wird von der Anordnung des Motors, von der Beladung sowie vom Radstand und der Spurweite bestimmt (Bild 8).
Radstand
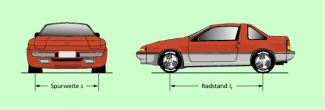
Als Radstand wird der Abstand von der Mitte der Vorderachse bis zur Mitte der Hinterachse bezeichnet (Bild 8).
Ein im Vergleich zur Länge des Fahrzeuges großer Radstand gestattet eine günstige Unterbringung der Fahrgäste zwischen den Achsen und verringert den Einfluss der Beladung auf die Lastverteilung. Die Tendenz zu Nickschwingungen verringert sich und eine weichere Federung (erhöhter Fahrkomfort) lässt sich ermöglichen.
Ein kurzer Radstand erleichtert die Kurvengängigkeit, d. h. bei gleichem Einschlagwinkel der Räder ergibt sich ein kleinerer Wendekreis. Als Anhaltspunkt kann die Verhältniszahl
dienen, die so groß wie möglich sein sollte. In der nachfolgenden Übersicht sind einige charakteristische Werte angegeben.
| Fahrzeugklasse | Verhältnissklasse k |
| Coupé | z.T. unter 0,56 |
| Kombilomousine | 0,57 - 0,67 |
| Stufenhecklimousine | 0,56 - 0,61 |
| Kleinwagen | bis 0,69 |
Spurweite
Als Spurweite bezeichnet man den Abstand von der Mitte des linken zur Mitte des rechten Vorderrades bzw. von der Mitte des linken zur Mitte des rechten Hinterrades (Bild 8).
Die Spurweite hat maßgeblichen Einfluss auf das Kurvenverhalten des Fahrzeuges und seine Wankneigung. Sie soll möglichst groß sein, wird aber durch die Fahrzeugaußenmaße (z. B. Radkästen) begrenzt). Beim Pkw betragen die Spurweiten normalerweise
-
Radstand und Spurweite eines PKW
Achsbelastung
Die Verteilung der Gewichtskräfte des Fahrzeuges auf die Vorder- bzw. Hinterachse in Ruhe oder bei konstanter Geschwindigkeit wird statische Achsbelastung genannt. Beim Anfahren, Bremsen oder bei Kurvenfahrt spricht man von dynamischer Achsbelastung.
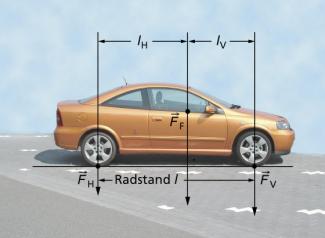
Bild 9 zeigt die statische Achsbelastung eines Autos. Die Verteilung der am Fahrzeugschwerpunkt angreifenden Gewichtskraft des Fahrzeugs auf die Auflagepunkte der Räder kann mit dem Hebelgesetz ermittelt werden:
Es ist dabei aber zu beachten, dass die Lage des Fahrzeugschwerpunkt von der Zuladung abhängt. Dadurch ergeben sich auch für die statische Achsverteilung Änderungen zum leeren Pkw (siehe Tabelle unten).
Um die allgemeinen physikalischen Zusammenhänge anschaulicher zu gestalten, werden sie jeweils immer auf denselben Pkw angewendet. Dieser wird im Folgenden charakterisiert:
| Für einen Pkw der unteren Mittelklasse mit Frontantrieb ergeben sich z. B. folgende Werte: | ||
| Höhe des Schwerpunktes (Massenmittelpunktes) | 0,60 m | |
| Spurweite | 1,30 m | |
| Radstand | 2,50 m | |
| Fahrzeugmasse (leer) | 900 kg | |
| Karosseriemasse | 700 kg | |
| In der nachfolgenden Übersicht sind durchschnittliche Maße und Achsbelastungen bei einem solchen Mittelklasse-Pkw angegeben. | ||
![]()
-
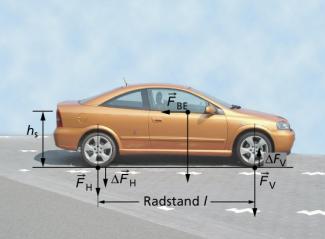
Achsbelastung bei einem stehenden oder mit konstanter Geschwindigkeit fahrenden Auto (statische Achsbelastung)
Beschleunigen
Bild 10 zeigt die dynamische Achsbelastung beim Beschleunigen eines Fahrzeuges. Durch das Beschleunigen (Anfahren) greift eine Trägheitskraft am Fahrzeugschwerpunkt an und bewirkt ein Drehmoment:
Dieses Drehmoment führt zur Drehung der Karosserie um den Drehpunkt D nach hinten und damit zur Entlastung der Vorderräder und Belastung der Hinterräder um die Kraft . Diese Kraft kann bis zur 30% der ursprünglichen Achslast betragen. Diese Entlastung der Vorderräder kann bei Pkw mit Frontantrieb beim Beschleunigen mit maximalen Drehmoment zum Durchdrehen der Räder führen.
Bremsen
In analoger Weise führt die Karosserie beim Bremsen eine Drehbewegung nach vorn aus, wodurch die Vorderräder mit einer zusätzlichen Kraft belastet und die Hinterräder entsprechend entlastet werden.
Für eine besondere Fahrsituationen soll die Wirkung dieser dynamischen Achsbelastung auf den Beispiel-Pkw untersucht werden:
Vollbremung auf einer ebenen, trockenen Betonstraße mit einem mit zwei Personen besetzten Mittelklasse-Pkw
Unter der Annahme, die gesamte Haftreibungskraft könnte zum Bremsen genutzt werden, gilt:
Damit ergibt sich eine zusätzliche Kraft:
Damit wird die Vorderachse mit
und die Hinterachse mit
belastet.
Bei einem normalen Pkw werden ungefähr 75 % der Bremskraft durch die Vorderradbremsen und 25 % durch die Hinterradbremsen aufgebracht. Diese kann aber bei dieser Belastung der Hinterachsen nicht auf die Straße übertragen werden, da gilt:
Die Hinterräder würden blockieren. Eine kleine Bodenunebenheit kann in dieser Situation zum Ausbrechen des Fahrzeuges führen. Da die im Schwerpunkt angreifende Trägheitskraft des Gesamtfahrzeuges hinter den noch wirksam bremsenden Rädern angreift, tritt ein sich selbst verstärkendes Giermoment auf, wenn der Pkw die Fahrtrichtung nur geringfügig verlässt.
-
Achsbelastung bei einem Fahrzeug, das beschleunigt wird (dynamische Achsbelastung)
Kurvenfahrt
Bild 11 zeigt die dynamische Achsbelastung bei Kurvenfahrt.
Beim Durchfahren einer Kurve mit konstanter Geschwindigkeit muss zur Überwindung der erhöhten Rollreibung (Faustregel: ) eine zusätzliche Kraft aufgebracht werden. Deshalb muss der Fahrer in Kurven das Gaspedal mehr durchtreten, um die Geschwindigkeit konstant zu halten.
Ein sicheres Durchfahren der Kurve ist aber nur dann möglich, wenn die auftretenden Zentrifugalkräfte durch die Haftreibungskräfte ausgeglichen werden können. Dazu müssen die Belastungen der einzelnen Räder untersucht werden.
Durch das Auftreten der Zentrifugalkraft (als Trägheitskraft) am Schwerpunkt tritt ein Drehmoment auf, das die Karosserie nach außen neigen lässt (Wanken). Dadurch werden die in der Kurve außen laufenden Räder mit einer zusätzlichen Kraft belastet und die innen laufenden Räder entsprechend entlastet. Es gilt:
| Für die jeweiligen Räder ergeben sich dann die folgenden Kräfte: | |||
| linkes Vorderrad: | rechtes Vorderrad: | ||
| linkes Hinterrad: | rechtes Hinterrad: | ||
Durchfährt der mit zwei Personen besetzte Beispiel-Pkw mit einer Geschwindigkeit v = 90 km/h eine Rechtskurve mit dem Radius r = 150 m, so treten folgende Radbelastungen auf: | |||
| linkes Vorderrad: | 4,68 kN | rechtes Vorderrad: | 1,44 kN |
| linkes Hinterrad: | 3,66 kN | rechtes Hinterrad: | 0,42 kN |
-
Dynamische Achsbelastung bei einer Kurvenfahrt

Die bei dieser Kurvenfahrt auftretende Zentrifugalkraft beträgt:
Diese muss anteilmäßig (entsprechend ihrer jeweiligen Belastung) von den einzelnen Rädern durch Haftreibung aufgebracht werden. Insbesondere gilt für das rechte Hinterrad:
Da diese Relation auch analog für die anderen Räder gezeigt werden kann, ist es möglich, die Kurve stabil zu durchfahren. Eine nur geringfügige Erhöhung der Geschwindigkeit von 90 km/h auf 105 km/h würde das rechte Hinterrad vollkommen entlasten, der Pkw würde bei Hinterradantrieb aus der Spur ausbrechen, da nur noch das linke Hinterrad eine Kraft auf die Straße überträgt.
Wird bei einer Kurvenfahrt zusätzlich noch gebremst, so tritt zu den bisher betrachteten Kräften eine weitere hinzu – die Bremskraft. Allen von den Reifen auf die Straße zu übertragenden Kräften muss eine entsprechende Gegenkraft, die Haftreibungreibungskraft, entgegenwirken, wenn das Fahrzeug sich stabil bewegen soll. Da die Haftreibung durch äußere Verhältnisse (Reifen, Fahrbahn) vorgegeben ist, ist sie maßgebend für die maximal übertragbare Kraft.
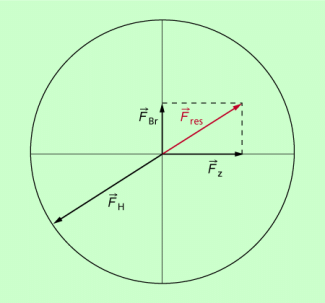
Das Zusammenwirken der Kräfte und ihre mögliche Größen lässt sich vereinfacht im sogenannten Kamm-Kreis (Bild 12) darstellen: Ist die resultierende Kraft größer als die Haftreibungskraft, dann beginnt das entsprechende Rad zu gleiten, die Fahrt wird instabil. Daraus ergibt sich, dass bei einer Kurvenfahrt die Bremskraft einen bestimmten Betrag nicht übersteigen darf:
Beispiel: Berechnung der maximalen Bremskraft für einen mit zwei Personen besetzten Beispiel-Pkw
Der Pkw fährt mit v = 90 km/h auf einer ebenen, trockenen Betonstraße (Haftreibungszahl 0,9) um eine Kurve mit dem Radius 150 m. Wir gehen vereinfacht von der gleichen Belastung aller Räder aus.
Bei Berücksichtigung der dynamischen Achsbelastung gilt:
Da das rechte Hinterrad am wenigsten belastet wird, kann von diesem auch die geringste Bremskraft übertragen werden.
Wird für die Größe in der Gleichung oben die scheinbar vom rechten Hinterrad zu tragende Masse
eingesetzt, so ergibt sich analog der obigen Rechnung für die maximal vom rechten Hinterrad übertragbare Bremskraft 0,33 kN. Unter Berücksichtigung, dass beide Hinterräder immer eine gleich große Bremskraft und zusammen in der Regel 25% der Gesamtbremskraft aufbringen, ergeben sich für die Bremskraft der einzelnen Räder und der Gesamtbremskraft folgende Werte:
| linkes Vorderrad: | 1,00 kN | rechtes Vorderrad: | 1,0 kN |
| linkes Hinterrad: | 0,33 kN | rechtes Hinterrad: | 2,66 kN |
Dieser Wert entspricht ungefähr nur 30% der maximalen Bremskraft, die dieser Pkw auf gerader Strecke aufbringen könnte
().
Ein normales (für diese Situation aber zu starkes) Bremsen würde zum Blockieren des rechten Hinterrades und damit zum Ausbrechen des Wagens aus der Spur führen. Dieses Verhalten wird durch ein Antiblockiersystem (ABS) verhindert.
-
Kamm-Kreis zur Ermittlung der Kräfteverhältnisse bei einer Kurvenfahrt