Stirlingscher Kreisprozess

Der stirlingsche Kreisprozess

Die ersten Maschinen zur Umwandlung von thermischer in mechanischer Energie waren Dampfmaschinen. In ihnen wird der als Arbeitsmittel verwendete Wasserdampf nacheinander in immer wiederkehrende Zustände überführt. Einen solchen Prozess, in dem der Ausgangszustand stets wieder erreicht wird, nennt man Kreisprozess. Die theoretische Beschreibung eines solchen Kreisprozesses erfolgte erstmals 1824 durch den französischen Ingenieur und Physiker SADI CARNOT (1796-1832).
Acht Jahre zuvor schon wurde dem schottischen Pfarrer ROBERT STIRLING (1790- 1878) ein Patent für den ersten Heißluftmotor zuerkannt. Dieser arbeitete mit Luft als Antriebsmittel und in einem ähnlichen Kreisprozess wie die Dampfmaschinen, dem stirlingschen Kreisprozess.
Das Ziel Robert STIRLINGs war es,

• den Wirkungsgrad der Dampfmaschinen zu verbessern und
• den „gefährlichen“ Wasserdampf als Antriebsmittel zu ersetzen.

Beides wurde durch seine genialen Erfindungen erreicht, auch wenn sich der Stirling-Motor bis heute nicht durchsetzen konnte bzw. nur in sehr speziellen Bereichen genutzt wird.

Beschreibung des stirlingschen Kreisprozesses

Der in STIRLING-Motoren (Heißluftmotoren) ablaufende stirlingsche Kreisprozess besteht aus je zwei isothermen und isochoren Zustandsänderungen, die nacheinander durchlaufen werden. Das als Antriebsmittel dienende Gas (Luft oder das heute verwendete Helium) wird als ideales Gas betrachtet und die Prozessführung als reversibel angenommen.
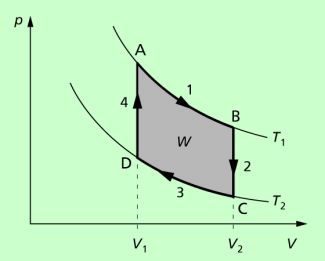
Wird der Prozess in seine vier Teilprozesse zerlegt, kann anhand des p-V-Diagramms die Arbeitsweise eines STIRLING-Motors erläutert werden.

(1) Isotherme Expansion: Im Ausgangspunkt A hat das als Arbeitsmittel dienende Gas
$\begin{array}{l}\text{die hohe Temperatur}{T}_1\text{, den höchsten Druck}{p}_1\\ \text{und das Volumen}{V}_1\text{.}\end{array}$
Um eine Expansion bei konstanter Temperatur zu realisieren, muss dem Gas eine Wärme $Q_1$zugeführt werden. Diese wird einem heißen äußeren Wärmespeicher entnommen. Beim Übergang in den Zustand B vergrößert das Gas sein Volumen. Dabei wird Arbeit verrichtet, der Kolben bewegt sich nach außen. Während die Temperatur bei diesem Teilprozess konstant bleibt, verringert sich der Druck. Die für die Zustandsänderung zugeführte Wärme ist:

$Q_1=N\cdot k\cdot T_1\cdot \ln \frac{V_2}{V_1}$

(2) Isochore Abkühlung: Im Punkt B wird die Wärmezufuhr gestoppt und das Gas auf die Temperatur $T_2$ abgekühlt. Dazu wird die Wärme $Q_2$ nach außen abgegeben. Dieser Vorgang erfolgt ohne Volumenänderung, sodass keine Arbeit verrichtet wird. Im Zustand C erreicht das Gas den kleinsten Druck.
Die dabei pro Mol des Gases abgegebene Wärme ist.

$\begin{array}{l}{Q}_2=C_{\text{V}}\left(T_2-T_1\right)\\ C_{\text{V}}\text{molare Wärmekapazität}\\ \text{bei konstantem Volumen}\\ T\text{absolute Temperatur}\end{array}$

(3) Isotherme Kompression: Beim Übergang C nach D wird bei konstanter Temperatur das Volumen des Gases auf verringert. Dabei erhöht sich der Druck. Für diesen Teilprozess muss Arbeit aufgewendet werden. Die dabei entstehende Wärme wird an einen kalten äußeren Wärmespeicher (Umgebung) abgeführt.
Die abgegebene Wärme beträgt:

$Q_3=N\cdot k\cdot T_2\cdot \ln \frac{V_2}{V_1}$

(4) Isochore Erwärmung: Im Punkt D hat das Gas sein Ausgangsvolumen erreicht und wird nun wieder auf die Temperatur $T_1$ erwärmt. Dazu wird bei konstantem Volumen Wärme zugeführt. In diesem Teilprozess erhöht sich der Druck. Das Gas befindet sich wieder im Ausgangszustand A.

Die bei den isochoren Zustandsänderungen abgeführte und zugeführte Wärmen sind gleich groß, da jeweils die gleiche Menge Gas abgekühlt bzw. erwärmt wird. Die nach außen abgegebene Arbeit ergibt sich aus der Differenz der zugeführten und abgegebenen Wärmen bei den isothermen Teilprozessen:

$W=Q_1-Q_2$

Dabei ist $Q_1>Q_2$, da die isotherme Expansion bei höherer Temperatur erfolgt als die isotherme Kompression.
Die mechanische Arbeit, die von einem STIRLING-Motor verrichtet werden kann, ist durch die von den Isothermen und Isochoren eingeschlossenen Fläche bestimmt. Sie kann durch Veränderung der Temperatur- und Volumendifferenzen variiert werden.

Wirkungsgrad eines Stirling-Motors

Der Wirkungsgrad eines STIRLING-Motors wird bestimmt von dem Verhältnis der abgegebenen mechanischen Arbeit W zur zugeführten Wärme $Q_1$:

$\eta =\frac{Q_1-Q_2}{Q_1}=1-\frac{Q_2}{Q_1}$

Für den als reversibel angenommenen Prozess ergibt sich damit mit

$\eta =1-\frac{T_2\cdot \ln \left(V_2/V_1\right)}{T_1\cdot \ln \left(V_2/V_1\right)}=1-\frac{T_2}{T_1}$

der gleiche Wirkungsgrad wie bei einem carnotschen Kreisprozess, also der maximale Wirkungsgrad für Kreisprozesse.
In der Praxis erreichten die STIRLING-Motoren aber einen größeren Wirkungsgrad als die Dampfmaschinen, da die Temperaturdifferenz bei Gasen leichter zu erhöhen ist als bei Wasserdampf. Die hohen Temperaturunterschiede verursachten aber einen großen Materialverschleiß, der die Wirtschaftlichkeit der Stirling-Motoren stark beeinträchtigte.