Energieerhaltungssatz der Mechanik

Der Energieerhaltungssatz der Mechanik ist ein spezieller Fall des allgemeinen Energieerhaltungssatzes. Er lautet:

In einem abgeschlossenen Bereich (abgeschlossenen System) gilt unter der Bedingung, dass keine Umwandlung von mechanischer Energie in andere Energieformen erfolgt:
Die Summe aus potenzieller Energie und kinetischer Energie eines Körpers ist konstant.

$\begin{array}{l}{E}_{\text{pot}}+E_{\text{kin}}=\text{konstant oder}\\ \Delta \text{(}{E}_{\text{pot}}+E_{\text{kin}})=0\end{array}$

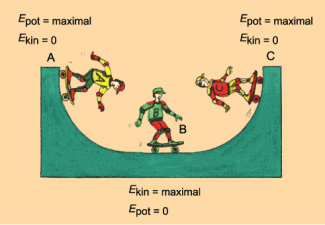
Das kann man z. B. bei einer Skateboard-Bahn kurzzeitig beobachten (Bilder 1 und 2): Die zunächst vorhandene potenzielle Energie wird in kinetische Energie und diese wieder in potenzielle Energie umgewandelt. Das wiederholt sich ständig.

Andere Beispiele für die Umwandlung von mechanischen Energieformen ineinander sind das Trampolinspringen, das Schaukeln, die Hin- und Herbewegung eines Pendels, ein nach oben geworfener Ball oder eine von einem Sprungbrett ins Wasser springende Person.

Grenzen der Anwendbarkeit des Energieerhaltungssatzes der Mechanik

Die Grenzen der Anwendbarkeit ergeben sich aus den Gültigkeitsbedingungen. Der Energieerhaltungssatz der Mechanik gilt nur unter der Bedingung, dass ein abgeschlossener Bereich (abgeschlossenes System) vorliegt und in diesem Bereich keine mechanische Energie in andere Energieformen umgewandelt wird.
Das gilt näherungsweise und für kurze Zeiträume für die oben genannten Beispiele. Es gilt auch für ein Fadenpendel, einen Federschwinger oder einen frei fallenden Körper, wenn man kurze Zeiträume betrachtet.

Bei vielen anderen Vorgängen, z. B. beim Fahren eines PKW, beim Rutschen eines Körpers auf einer geneigten Ebene oder beim Bergabfahren mit dem Fahrrad tritt Reibung auf. Das gilt auch für ein Fadenpendel oder einen Federschwinger, wenn man sie längere Zeit sich selbst überlässt.
Durch Reibung wird ein Teil der mechanischen Energie in thermische Energie umgewandelt. Die formale Anwendung des Energieerhaltungssatzes würde dann zu falschen Ergebnissen führen.
Wenn man ihn anwenden will, muss jeweils geprüft werden, ob seine Gültigkeitsbedingungen zumindest näherungsweise für den betrachteten Fall erfüllt sind.

Beispiele für die Anwendung des Energieerhaltungssatzes der Mechanik

Für einige spezielle Fälle kann der Energieerhaltungssatz der Mechanik genutzt werden, um Sachverhalte zu erklären und physikalische Größen zu berechnen. Wir betrachten nachfolgend drei ausgewählte Beispiele.

(1) Umwandlung mechanischer Energieformen ineinander

Erkläre, weshalb eine aus bestimmter Höhe auf ein Trampolin treffende Person annähernd wieder die gleiche Höhe erreicht!

In einer bestimmten Höhe besitzt eine Person potenzielle Energie gegenüber dem Trampolin. Beim Fall wird diese potenzielle Energie in kinetische Energie umgewandelt. Das Trampolin wird elastisch verformt und wirkt so, dass die Person wieder nach oben geschleudert wird. Dabei wird kinetische Energie in potenzielle Energie umgewandelt. Da bei diesem Vorgang nur wenig mechanische Energie in thermische Energie umgewandelt wird, erreicht die Person nach dem Energieerhaltungssatz der Mechanik näherungsweise wieder die gleiche Höhe.

(2) Geschwindigkeit beim freien Fall

Eine Person springt aus 5 m Höhe ins Wasser. Mit welcher Geschwindigkeit trifft sie auf der Wasseroberfläche auf?

Analyse:
Die Person besitzt zunächst potenzielle Energie. Diese wird beim Sprung fast vollständig in kinetische Energie umgewandelt. Die Reibung (Luftwiderstand) kann in diesem Fall vernachlässigt werden.

Lösung:

$\begin{array}{l}m\cdot g\cdot h=\frac{1}{2}m\cdot v^2\\ g\cdot h=\frac{1}{2}{v}^2\\ v=\sqrt{2g\cdot h}\\ v=\sqrt{2\cdot \mathrm{9,81}\frac{\text{m}}{{\text{s}}^{\text{2}}}\cdot 5\text{ m}}\\ v=\mathrm{9,9}\frac{\text{m}}{\text{s}}=36\frac{\text{km}}{\text{h}}\end{array}$

Ergebnis:
Eine Person, die aus 5 m Höhe springt, trifft mit einer Geschwindigkeit von 36 km/h auf der Wasseroberfläche auf.
Beachte: Die Geschwindigkeit ist unabhängig davon, ob die Person eine große oder eine kleine Masse hat.

(3) Höhe bei bestimmter Abwurfgeschwindigkeit

Ein Stein wird mit einer Geschwindigkeit von 10 m/s senkrecht nach oben geworfen. Welche maximale Höhe erreicht er?

Analyse:
Die kinetische Energie des Steines wird in potenzielle Energie umgewandelt. Im höchsten Punkt seiner Bahn ist die kinetische Energie null, die potenzielle Energie maximal. Die Reibung kann für diesen Vorgang vernachlässigt werden.

Lösung:

$\begin{array}{l}\frac{1}{2}m\cdot v^2=m\cdot g\cdot h\\ \frac{1}{2}{v}^2=g\cdot h\\ h=\frac{v^2}{2g}\\ h=\frac{{(10\frac{\text{m}}{\text{s}})}^2}{2\cdot \mathrm{9,81}\frac{\text{m}}{{\text{s}}^{\text{2}}}}\\ h=\mathrm{5,1}\text{ m}\end{array}$

Ergebnis:
Bei einer Abwurfgeschwindigkeit von 10 m/s erreicht der Stein eine maximale Höhe von 5,1 m.
Beachte: Die maximale Höhe hängt nur von der Anfangsgeschwindigkeit ab. Sie ist unabhängig davon, welche Masse der Körper hat.