Gravitation

Alle Körper ziehen sich aufgrund ihrer Massen gegenseitig an. So zieht z.B. die Erde den Mond an. Umgekehrt zieht auch der Mond die Erde an.
Die gegenseitige Anziehung von Körpern aufgrund ihrer Massen wird Massenanziehung oder Gravitation (gravis, lat.: schwer) genannt. Die dabei wirkenden Kräfte werden als Schwerkräfte oder als Gravitationskräfte bezeichnet.

Bekannt sind vor allem die Gravitationskräfte zwischen der Erde und auf ihr befindlichen Körpern. Diese Erdanziehungskraft bewirkt, dass ein Apfel, wenn man ihn loslässt, senkrecht nach unten fällt. Ein Schrank drückt auf seine Unterlage, den Boden. Ein Kind, das auf einer Schaukel sitzt, zieht an der Aufhängung der Schaukel.

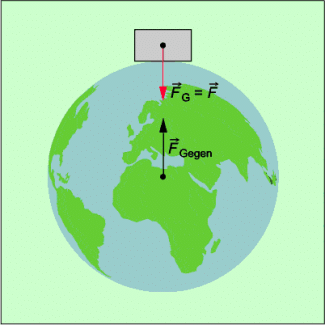
Die Erdanziehungskraft wird häufig auch als Gewichtskraft bezeichnet. Die Gewichtskraft ist die Gravitationskraft, mit der ein Körper von der Erde angezogen wird (Bild 2).
Jeder Körper auf der Erdoberfläche oder in der Nähe der Erde wird von dieser angezogen. Zugleich zieht auch jeder Körper die Erde an. Diese Kraft ist nach dem Wechselwirkungsgesetz der Gewichtskraft entgegen gerichtet und hat den gleichen Betrag. Wenn also z. B. deine Gewichtskraft 620 N beträgt, dann wirst du mit einer Kraft von 620 N von der Erde angezogen. Zugleich ziehst du die Erde mit genau dieser Kraft an.

Gravitationskräfte wirken nicht nur zwischen der Erde und dem Mond oder zwischen der Erde und auf ihr befindlichen Körpern. Gravitation tritt vielmehr zwischen beliebigen Körpern auf, die eine Masse besitzen. Häufig sind aber die dabei auftretenden Gravitationskräfte so klein, dass man sie vernachlässigen kann. So beträgt z. B. die Gravitationskraft zwischen zwei Personen, die je eine Masse von 50 kg haben und die sich in einem Abstand von 1 m voneinander befinden, etwa F = 0,000 000 007 N.

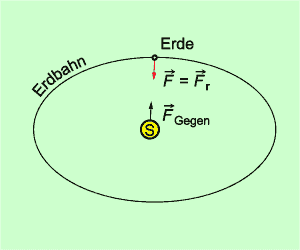
Gravitationskräfte bestimmen auch die Bewegung von Himmelskörpern sowie von künstlichen Satelliten und Raumstationen. So bewegt sich z. B. die Erde auf einer näherungsweise kreisförmigen Bahn um die Sonne (Bild 3). Der Mond oder künstliche Satelliten bewegen sich um die Erde. Damit sich aber ein Körper auf einer kreisförmigen Bahn bewegt, muss eine Kraft in Richtung des Zentrums der Bewegung wirken (Radialkraft oder Zentralkraft). Diese Kraft ist die Gravitationskraft, die die Sonne bzw. die Erde auf die Körper ausübt, die sich um sie bewegen.