Radialkraft
Die Radialkraft gibt an, mit welcher Kraft ein Körper auf einer Kreisbahn gehalten wird.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Radialkraft, auch Zentralkraft oder Zentripetalkraft genannt, kann mit folgenden Gleichungen berechnet werden:
Sie ist, wie jede andere Kraft, eine gerichtete (vektorielle) Größe und immer in Richtung Zentrum der Kreisbewegung gerichtet.
Damit sich ein Körper auf einer Kreisbahn bewegt, muss auf ihn eine Kraft in Richtung des Zentrums der Kreisbewegung (in Richtung des Radius) wirken. Diese Kraft wird als Radialkraft bezeichnet.
Die Radialkraft gibt an, mit welcher Kraft ein Körper auf einer Kreisbahn gehalten wird.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Radialkraft, auch Zentralkraft oder Zentripetalkraft genannt, kann mit folgenden Gleichungen berechnet werden:
| m | Masse des Körpers | |
| v | Geschwindigkeit des Körpers | |
| r | Radius der Kreisbahn | |
| T | Umlaufzeit | |
| n | Drehzahl |
Die Radialkraft ist, wie jede andere Kraft, eine gerichtete (vektorielle) Größe und immer in Richtung Zentrum der Kreisbewegung gerichtet. Sie bewirkt eine Beschleunigung in dieser Richtung. Diese radial gerichtete Beschleunigung wird als Radialbeschleunigung oder Zentralbeschleunigung bezeichnet.
-
Sybille Storch, Berlin
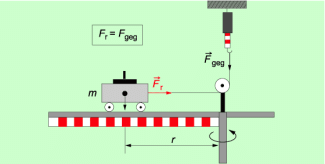
Experimentell kann man die für die Radialkraft geltenden Zusammenhänge mit einem Radialkraftmesser bestimmen (Bild 2).
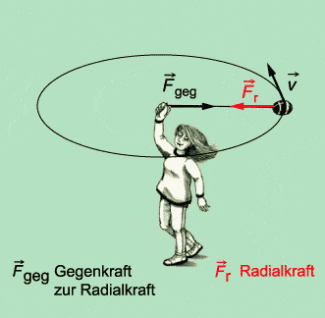
Zu jeder Radialkraft gibt es eine Gegenkraft, die z. B. beim Herumschleudern eines Körpers als Zugkraft an der Hand zu spüren ist. Nach dem Wechselwirkungsgesetz ist diese Gegenkraft genauso groß wie die Radialkraft, aber entgegengesetzt gerichtet.
Die Radialkraft spielt bei Kurvenfahrten sowie bei der Bewegung von Satelliten, Monden und Planeten eine wichtige Rolle.
Bei Kurvenfahrten wird die Radialkraft durch die Reibung zwischen Reifen und Straße aufgebracht. Bei Zweiradfahrzeugen (Fahrräder, Motorräder) spielt auch die Neigung des Fahrzeuges eine Rolle.
Bei Satelliten um die Erde oder beim Erdmond ist die Radialkraft die Gravitationskraft, die die Erde auf die betreffenden Himmelskörper ausübt. Bei Planeten ist die Radialkraft die Gravitationskraft, die die Sonne auf die Planeten ausübt.
Bei einem Karussell wird die erforderliche Radialkraft durch die Aufhängung der Gondel aufgebracht. Bei Loopingbahnen muss die Bahn selbst die Radialkraft für die Kreisbewegung aufbringen.
-

pdesign - Fotolia.com