Kosmische Geschwindigkeiten
Die Geschwindigkeiten, die ein Körper mindestens erreichen muss, um von einem Himmelskörper aus auf eine Bahn um diesem Himmelskörper zu gelangen oder um diesen Himmelskörper zu verlassen, bezeichnet man als kosmische Geschwindigkeiten. Unterschieden wird zwischen
- der 1. kosmischen Geschwindigkeit (minimale Keisbahngeschwindigkeit),
- der 2. kosmischen Geschwindigkeit (Fluchtgeschwindigkeit) und
- der 3. kosmischen Geschwindigkeit.
Kosmische Geschwindigkeiten
Die Geschwindigkeiten, die ein Körper mindestens erreichen muss, um von einem Himmelskörper aus auf eine Bahn um diesem Himmelskörper zu gelangen oder um diesen Himmelskörper zu verlassen, bezeichnet man als kosmische Geschwindigkeiten. Unterschieden wird zwischen
- der 1. kosmischen Geschwindigkeit (minimale Keisbahngeschwindigkeit),
- der 2. kosmischen Geschwindigkeit (Fluchtgeschwindigkeit) und
- der 3. kosmischen Geschwindigkeit.
1. kosmische Geschwindigkeit
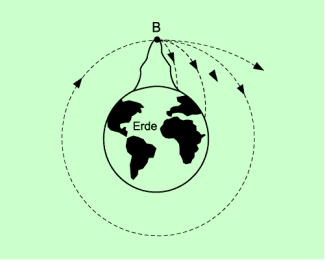
Damit ein Satellit in eine Kreisbahn um die Erde oder einen anderen Himmelskörper gelangt, muss er eine bestimmte Mindestgeschwindigkeit erreichen. Diese Geschwindigkeit wird als 1. kosmische Geschwindigkeit oder als minimale Kreisbahngeschwindigkeit bezeichnet.
Für die 1. kosmische Geschwindigkeit gilt allgemein:
Für die Erde hat die 1. kosmische Geschwindigkeit einen Wert von 7,9 km/s. Mithilfe der genannten Gleichung können auch die 1. kosmischen Geschwindigkeiten für andere Himmelskörper berechnet werden.
2. kosmische Geschwindigkeit
Die 2. kosmische Geschwindigkeit ist die Geschwindigkeit, die ein Körper erreichen muss, wenn er den Anziehungsbereich eines Himmelskörpers verlassen soll. Sie wird deshalb auch als Fluchtgeschwindigkeit bezeichnet. Diese Geschwindigkeit ist z. B. erforderlich, wenn von der Erde aus eine Raumsonde zum Mond oder zum Mars oder zu einem anderen Himmelskörper fliegen soll.
Für die 2. kosmische Geschwindigkeit gilt:
Für die Erde hat die 2. kosmische Geschwindigkeit einen Wert von 11,2 km/s. Sie ist also etwa 1,4-mal größer als die 1. kosmische Geschwindigkeit.
3. kosmische Geschwindigkeit
Die Geschwindigkeit, die erforderlich ist, damit ein Körper unser Sonnensystem verlässt, wird als 3. kosmische Geschwindigkeit bezeichnet. Eine Abschätzung der 3. kosmischen Geschwindigkeit kann mit folgender Gleichung vorgenommen werden:
Geht man von einer erdgebundenen Betrachtung aus, so gilt: Ohne Berücksichtigung der Erdbewegung beträgt die 3. kosmische Geschwindigkeit für die Erde 42,4 km/s. Wird ein Körper in Richtung der Bahngeschwindigkeit der Erde sowie in ihrer Drehrichtung abgeschossen, so beträgt diese Geschwindigkeit 16,7 km/s.