Absolute Entropien und der 3. Hauptsatz der Thermodynamik

Um einen vergleichbaren Standard für die verschiedenen thermodynamischen Werte zu erhalten, ist die Definition eines gültigen Bezugszustands notwendig. So wurde die Standardbildungsenthalpie der Elemente in ihren Standardzuständen unter Standardbedingungen gleich Null gesetzt. Eine solche einfache Definition kann für die Entropie nicht gemacht werden, da unterschiedliche Elemente, wie Sauerstoff, Quecksilber und Kupfer, bei 25 °C einen unterschiedlichen Aggregatzustand (gas, flüssig, fest) und somit auch einen unterschiedlichen Grad an Ordnung besitzen.
Aus der Definition der Entropie und der Grundgleichung der Wärmelehre bei konstantem Volumen ergibt sich:

$\begin{array}{l}\text{Entropie:}\Delta S=\frac{q}{T}\\ \text{Wärme:}q=C_v·\Delta T\\ \Delta S_v=\frac{C_v}{T}·\Delta T\\ S_v(T_{\text{a}})–S_v(0)=\frac{C_v}{T}·(T_{\text{a}}–T_0)\end{array}$

S: Entropie (Ordnungszustand des Systems
q: Wärmemänge
T: Temperatur
Cv: stoffspezifische Wärmekapazität, bei konstanntem Volumen

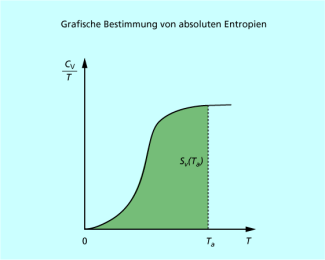
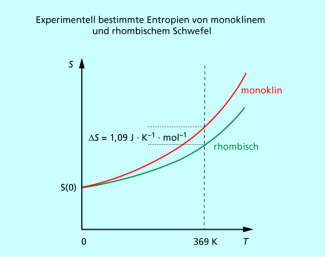
Die Entropie eines Systems bei einer bestimmten Temperatur $T_{\text{a}}$ kann somit aus der Messung der Wärmekapazität bei tiefen Temperaturen kurz oberhalb des absoluten Nullpunkts $T_0$ bis zur gewünschten Temperatur $T_{\text{a}}$ grafisch bestimmt werden (Bild 1). Bei derartigen Untersuchungen fand W. NERNST 1906, dass rhombischer und monokliner Schwefel bei sehr tiefen Temperaturen die gleiche Entropie besitzen (Bild 2).
Diese Beobachtungen, die später auch für andere Substanzen gemacht worden sind, sind im dritten Hauptsatz der Thermodynamik, der auch als Nernst-Theorem bezeichnet wird, zusammengefasst.

Alle perfekten kristallinen Substanzen besitzen die gleiche Entropie am absoluten Nullpunkt (T = 0 K). Der absolute Nullpunkt kann experimentell für keine Substanz erreicht werden.

In einem perfekten Kristall (Bild 3) befindet sich jedes Atom an seinem fest definierten Platz. Dies findet man theoretisch nur am absoluten Nullpunkt der Temperatur. Jede Bewegung ist eingefroren. Da die Entropie ein Maß für die Unordnung eines Systems darstellt, postulierte MAX PLANCK:

Die Entropie aller perfekten kristallinen Substanzen am absoluten Nullpunkt ist gleich Null: S(0) = 0.

Die heute am gebräuchlichsten Form des dritten Hauptsatzes wurde von G. N. LEWIS und M. RANDALL formuliert:

Jede Substanz besitzt eine endliche, positive Entropie. Diese kann gleich Null sein am absoluten Nullpunkt. Sie ist gleich Null für alle perfekten kristallinen Substanzen.

Auch aus der Definition der Entropie nach LUDWIG BOLTZMANN

S = k ln W,

in der W ein Maß für die Verteilung des Systems auf verschiedene mögliche Zustände darstellt, ergibt sich die Entropie eines perfekten Kristalls zu Null, da es nur eine mögliche Anordnung der Atome im perfekten Kristall gibt (W = 1).

Entropiewerte sind demzufolge als absolute molare Entropiewerte $S^0\text{(298}\text{K)}$ unter Standardbedingungen (1 bar, 25 °C) tabelliert. Sie ergeben sich als absolute Werte aus der Bestimmung der Entropie der jeweiligen Substanz von 0 K bis zu dem jeweils stabilsten Zustand bei 1 bar und 25 °C. Aus diesen tabellierten Werten können sehr einfach die Standardreaktionsentropien berechnet werden.

Betrachtet man die Werte in obiger Tabelle, so besitzt die Kohlenstoffmodifikation Grafit aufgrund ihrer Schichtstruktur eine höhere Entropie als Diamant, in dessen Gitter alle Atome tetraedrisch angeordnet sind. Andere Festkörper bestehen aus Molekülen, wie z. B. Glucose, sie haben viele verschiedene Anordnungs- und Orientierungsmöglichkeiten, sodass sie eine höhere Entropie aufweisen. Des Weiteren ist die Entropie wie zu erwarten für Gase deutlich größer als für Flüssigkeiten und Festkörper. Dieses Verhalten lässt sich auch sehr gut anhand der Entropiewerte für Eis, Wasser und Wasserdampf aus der Tabelle erkennen.