pH-Wert – Definition und Berechnung

Begriffsdefinition

Der pH-Wert ist ein Maß dafür, wie sauer bzw. basisch eine Lösung ist. Dies hängt von der Konzentration der Wasserstoff-Ionen (${\text{H}}^{\text{+}}$) bzw. Hydronium-Ionen (${\text{H}}_{\text{3}}{\text{O}}^{+}$)in der Lösung ab.
Um besser handhabbare Zahlenwerte für die Konzentration der Wasserstoff-Ionen zu erhalten wurde, der pH-Wert definiert als negativer dekadischer Logarithmus der Konzentration der Wasserstoff-Ionen bzw. Hydronium-Ionen.
(Hinweis: Da nur Zahlenwerte, jedoch keine Einheiten logarithmiert werden können, bezieht man die Konzentration immer auf die Standardkonzentration von 1 $\text{mol}\cdot {\text{l}}^{-1}$.

$pH\text{= -}\lg c{\text{(H}}^{\text{+}})\text{bzw}\text{.}pH\text{= -}\lg c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}})$

In analoger Weise lässt sich auch ein pOH-Wert definieren, als negativer dekadischer Logarithmus der Konzentration von ${\text{OH}}^{-}$-Ionen.

$pOH\text{= -}\lg c{\text{(OH}}^{-})$

Das Ionenprodukt des Wassers und der pH-Wert

Wasser leitet sehr geringfügig den elektrischen Strom. Die Ursache dafür liegt in der Eigendissoziation des Wassers, der Autoprotolyse.

$\begin{array}{c}{\text{H}}_{\text{2}}\text{O}\rightleftharpoons {\text{H}}^{\text{+}}{\text{+ OH}}^{\text{-}}bzw.\\ {\text{H}}_{\text{2}}{\text{O + H}}_{\text{2}}\text{O}\rightleftharpoons {\text{H}}_{\text{3}}{\text{O}}^{\text{+}}{\text{+ OH}}^{\text{-}}\end{array}$

Für diese Gleichgewichtsreaktion lässt sich das Massenwirkungsgesetz (MWG) aufstellen.

$\text{K=}\frac{c({\text{H}}^{+})\cdot c({\text{OH}}^{-})}{c{\text{(H}}_{\text{2}}\text{O)}}bzw.\text{K=}\frac{c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{)}\cdot c({\text{OH}}^{-})}{c({\text{H}}_{\text{2}}\text{O})\cdot c({\text{H}}_{\text{2}}\text{O})}$

Dieses Gleichgewicht liefert nach dem MWG die temperaturabhängige Gleichgewichtskonstante K. Da die Dissoziation so gering ist, d. H. das Gleichgewicht bei der Autoprotolyse weit auf der Seite des Wassers liegt, kann die Konzentration des Wassers als konstant angesehen werden. Sie lässt sich so in die Gleichgewichtskonstante einbeziehen. Die Konstante $K_W$ wird als das Ionenprodukt des Wassers bezeichnet.

$K_{\text{w}}\text{=}c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{)}\cdot c{\text{(OH}}^{\text{-}}\text{)}$

Bei 22°C beträgt das Ionenprodukt des Wassers ${\text{10}}^{\text{-14}}{\text{mol}}^{\text{2}}\cdot {\text{l}}^{-2}$.

$c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{)}\cdot c{\text{(OH}}^{\text{-}}\text{) =}{K}_{\text{w}}{\text{= 10}}^{\text{-14}}{\text{mol}}^{\text{2}}\cdot {\text{l}}^{\text{-2}}$

Logarithmiert man diese Gleichung, ergibt sich unter Berücksichtigung der Definitionen des pH-Werts und des pOH-Werts:

$pH+pOH=p{K}_w=14$

Da in reinem Wasser nach der Reaktionsgleichung für die Autoprotolyse die Konzentration der ${\text{H}}_{\text{3}}{\text{O}}^{+}$-Ionen gleich der Konzentration an ${\text{OH}}^{-}$-Ionen ist, ergibt sich für den pH-Wert des reinen Wassers:

pH = 7

Dieser pH-Wert von 7 wird auch als neutral bezeichnet. Bei höheren Konzentrationen von ${\text{H}}_{\text{3}}{\text{O}}^{+}$-Ionen ergeben sich dementsprechend niedrigere pH-Werte (saurer Bereich), bei geringeren ${\text{H}}_{\text{3}}{\text{O}}^{+}$- Konzentrationen ist der pH-Wert größer als 7 (basischer Bereich).

Im Alltag begegnen uns eine Reihe von sauren und basischen Lösungen, die dementsprechend einen unterschiedlichen pH-Wert aufweisen.

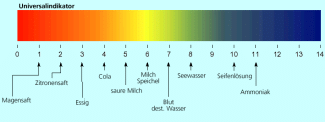
Universalindikatoren zeigen den pH-Wert einer Lösung durch ihre charakteristische Färbung an. So führt ein saurer pH-Wert bei Universalindikatoren wie Unitest zu einer roten Färbung und ein basischer pH-Wert zu einer blauen Färbung. Im neutralen Bereich sind Universalindikatoren gelblich/grün gefärbt (vgl. Bild 1). Es gibt allerdings verschiedene Säure-Base-Indikatoren, die andere Farbreaktionen zeigen. Ihre „Umschlagsbereiche“, bei denen sie die Farbe ändern, müssen nicht zwangsläufig bei einem pH-Wert von 7 liegen.

Berechnungen von pH-Werten verschiedener Lösungen

pH-Wert starker Säuren und Basen
Bei Lösungen starker Säuren und Basen ist die Berechnung des pH-Wertes denkbar einfach. Starke Säuren und Basen liegen praktisch vollständig dissoziiert vor. Damit ist die Konzentration der ${\text{H}}_{\text{3}}{\text{O}}^{+}$-Ionen bzw. der ${\text{OH}}^{-}$-Ionen gleich der ursprünglichen Konzentration $c_0$ der eingesetzten Säure.

Für eine wässrige Lösung einer einwertigen starken Säure, z. B. Salzsäure, der Konzentration von 0,01 mol/l gilt somit:

$\begin{array}{l}{\text{HA + H}}_{\text{2}}\text{O}\to {\text{H}}_{\text{3}}{\text{O}}^{\text{+}}{\text{+ A}}^{\text{-}}\\ c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{) =}{c}_0\text{(HA)}\\ c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{) = 0}{\text{,01 mol/l = 10}}^{\text{-2}}\text{mol/l}\\ pH\text{= -lg}c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{) = 2}\end{array}$

Bei mehrwertigen starken Säuren muss dazu noch berücksicht werden, dass ein Säuremolekül mehrere Wasserstoff-Ionen abgibt. Für eine Schwefelsäure der gleichen Konzentration von 0,01 mol/l ergibt sich ein pH-Wert von ca. 1,7! Die Konzentration an Hydroniumionen beträgt natürlich 0,02 mol/l bei vollständiger Dissoziation der Säure.

Für starke Basen berechnet man den pH-Wert aus dem pOH-Wert über das Ionenprodukt des Wassers in ansonsten ähnlicher Weise.

$\begin{array}{l}pOH=-\lg c({\text{OH}}^{-})=-\lg c_0\\ pH=p{K}_W-pOH\text{=}\text{‌}\text{14}-pOH\\ pH=\text{‌}\text{14}+\lg c_0\\ (c_0\text{ist die Ausgangskonzentration der Base)}\end{array}$

pH-Wert schwacher Säuren und Basen
Schwache Säuren und Basen dissoziieren nicht vollständig. Man kann also nicht davon ausgehen, dass die Konzentration der ${\text{H}}^{\text{+}}$- bzw. ${\text{H}}_{\text{3}}{\text{O}}^{+}$-Ionen der Konzentration (Gesamtkonzentration) der Säure entspricht, da nur ein Teil der Säuremoleküle (HA) dissoziiert vorliegen. Das Ausmaß der Dissoziation und damit die Säurestärke hängt vom pKs-Wert der Säure ab.
Analog zum pH-Wert ist der pKs-Wert der negative dekadische Logarithmus der Säurekonstante $K_S$. Die Konstante $K_S$ ist die Gleichgewichtskonstante für die Dissoziation der Säure in Wasser. Aus dem MWG ergibt sich damit folgender Zusammenhang:

$\begin{array}{l}{\text{HA + H}}_{\text{2}}\text{O}\rightleftharpoons {\text{H}}_{\text{3}}{\text{O}}^{\text{+}}{\text{+ A}}^{\text{-}}\\ K_S´\text{=}\frac{c{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{)}\cdot c{\text{(A}}^{\text{-}}\text{)}}{c\text{(HA)}\cdot c{\text{(H}}_{\text{2}}\text{O)}}\end{array}$

da ja c(${\text{A}}^{-}$) = c(${\text{H}}_{\text{3}}{\text{O}}^{+}$) ist, ergibt sich:

$\begin{array}{c}{K}_S´\left[c{\text{(H}}_{\text{2}}\text{O)}\right]\text{=}\frac{c^2{\text{(H}}_{\text{3}}{\text{O}}^{\text{+}}\text{)}}{c\text{(HA)}}\text{=}{K}_S\\ K_S\left[c(\text{HA})\right]\text{=}{c}^2(H_3{O}^{+})\\ p{K}_S-\lg c(\text{HA})=2pH\\ \frac{p{K}_S-\lg c(\text{HA})}{2}\text{=}pH\end{array}$

In dieser Gleichung ist nur noch die Konzentration der Säure im Gleichgewicht c(HA) unbekannt. Sie ergibt sich aus der Differenz von der Ausgangskonzentration Säure und dem dissoziierten Anteil c(${\text{A}}^{-}$). Da verdünnte schwache Säuren so wenig dissoziieren, also c(${\text{A}}^{-}$) << c(HA) ist, kann man näherungsweise annehmen, dass die Ausgangskonzentration der Säure nahezu gleich der Konzentration der undissoziierten Säure im Gleichgewicht ist.

$\begin{array}{l}\text{Aus}c{\text{(A}}^{\text{-}}\text{) <<}c\text{(HA) und}{c}_{\text{0}}\text{(HA) =}c{\text{(A}}^{\text{-}}\text{) +}c\text{(HA) folgt:}\\ \text{c(HA)}\approx c_{\text{0}}\text{(HA) (}{c}_{\text{0}}\text{ist die Ausgangskonzentration der Säure)}\end{array}$

Daraus ergibt sich für den pH-Wert von Lösungen schwacher Säuren folgende Näherungsgleichung:

$\begin{array}{l}pH=\frac{1}{2}\left[p{K}_S-\lg c_0(HA)\right]\text{bzw}.\\ c({\text{H}}_{\text{3}}{\text{O}}^{\text{+}})=\sqrt{K_S\cdot c_0\text{(HA)}}\end{array}$

Eine ähnliche Näherung erhält man für schwache Basen:

$\begin{array}{l}pOH=\frac{1}{2}\left[p{K}_B-\lg c_0(B)\right]\text{(bzw}\text{.}c({\text{OH}}^{\text{-}})=\sqrt{K_B\cdot c_0\text{(B)}})\\ \text{Daraus folgt:}\\ pH=p{K}_W-\frac{1}{2}\left[p{K}_B-\lg c_0(B)\right]\\ pH=14-\frac{1}{2}p{K}_B+\frac{1}{2}\lg c_0(B)\end{array}$

Dabei ist jedoch zu beachten, dass es sich um Näherungsgleichungen handelt, die nur für schwache Säuren oder Basen in ausreichender Verdünnung gilt. Wendet man diese Gleichung auf andere Lösungen an, erhält man falsche Ergebnisse (siehe Rechenbeispiel)!