Abstand zweier Ebenen

• Bezeichnet $P_1$ einen beliebigen Punkt von ${\epsilon }_1$ und $P_2$ einen beliebigen Punkt von ${\epsilon }_2$, so soll unter dem Abstand von ${\epsilon }_1$ und ${\epsilon }_2$ die kleinste aller möglichen Streckenlängen $\left|\overline{P_1{P}_2}\right|$ verstanden werden.

Sind ${\epsilon }_1$ und ${\epsilon }_2$ nicht zueinander parallel, so haben beide eine Schnittgerade g gemeinsam.

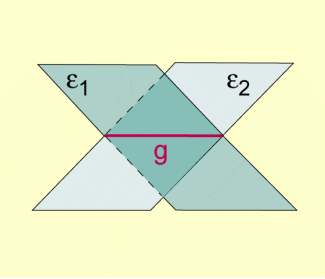
Wie beim Abstand zweier einander schneidender Geraden würde sich hier der Abstand 0 ergeben, obwohl ${\epsilon }_1$ und ${\epsilon }_2$ nicht zusammenfallen.
Aus diesem Grund betrachten wir im Weiteren nur zwei zueinander parallele Ebenen ${\epsilon }_1$ und ${\epsilon }_2$.

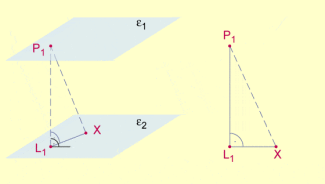
Wählt man einen Punkt $P_1$ von ${\epsilon }_1$ und fällt das Lot von $P_1$ auf ${\epsilon }_2$, dann bezeichnet $L_1$ den zugehörigen Lotfußpunkt. Aufgrund der Dreiecksungleichung ist $\left|\overline{P_1{L}_1}\right|$ die kürzeste unter allen Verbindungsstrecken, die $P_1$ mit einem Punkt X von ${\epsilon }_2$ verbinden.

Wir betrachten nun einen von $P_1$ verschiedenen Punkt $P_1^{*}$ in ${\epsilon }_1$. $L_1^{*}$bezeichnet dann den zugehörigen Lotfußpunkt in ${\epsilon }_2$ und $P_1{P}_1^{*}{L}_1^{*}{L}_1$ bildet ein Rechteck.

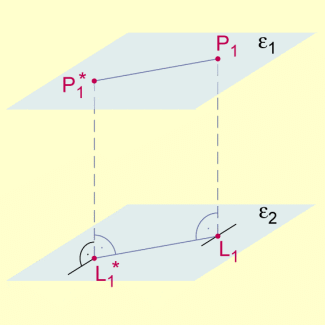
Daraus kann man schlussfolgern, dass die Bestimmung des Abstandes zweier paralleler Ebenen ${\epsilon }_1$ und ${\epsilon }_2$ unabhängig von der Wahl des Punktes $P_1$ von ${\epsilon }_1$ in ist.

Durch diese Überlegung lässt sich die Abstandsbestimmung für zwei zueinander parallele Ebenen auf die Bestimmung des Abstandes eines Punktes von einer Ebene zurückführen. Es gelten die folgenden beiden Sätze.

• Satz: Sind im Raum zwei zueinander parallele Ebene ${\epsilon }_1$ und ${\epsilon }_2$ jeweils durch einen Stützpunkt $P_1$ bzw. $P_2$ und jeweils einen Normalenvektor ${\overrightarrow{n}}_1$ bzw. ${\overrightarrow{n}}_2$ ( ${\overrightarrow{n}}_1$ und ${\overrightarrow{n}}_2$ sind linear abhängig voneinander) gegeben, so kann man den (vorzeichenbehafteten) Abstand der beiden Ebenen durch
  $h=\left({\overrightarrow{p}}_2-{\overrightarrow{p}}_1\right)\cdot \frac{{\overrightarrow{n}}_1}{\left|{\overrightarrow{n}}_1\right|}$ berechnen.

• Satz: Sind im Raum zwei zueinander parallele Ebene ${\epsilon }_1$ und ${\epsilon }_2$ durch ihre Gleichungen $ax+by+cz+d_1=0$ bzw. $ax+by+cz+d_2=0$ gegeben, so kann man den (vorzeichenbehafteten) Abstand der beiden Ebenen (beispielsweise) unter Verwendung der Koordinaten des Punktes $P_2\left(x_{P_2};y_{P_2};z_{P_2}\right)\in {\epsilon }_2$ durch $h=\frac{a{x}_{P_2}+b{y}_{P_2}+c{z}_{P_2}+d_1}{\sqrt{a^2+b^2+c^2}}$ bestimmen.

Berechnet man den Abstand von ${\epsilon }_1$ und ${\epsilon }_2$ wie oben angegeben, dann ist

• $h>0$ genau dann, wenn ${\epsilon }_2$ in dem Halbraum bezüglich ${\epsilon }_1$ liegt, in den der Normalenvektor ${\overrightarrow{n}}_1$ von ${\epsilon }_1$ zeigt;
• $h<0$ genau dann, wenn ${\epsilon }_2$ in dem Halbraum bezüglich ${\epsilon }_1$ liegt, in den der Normalenvektor ${\overrightarrow{n}}_1$ von ${\epsilon }_1$ nicht zeigt;
• h = 0 genau dann, wenn ${\epsilon }_1$ = ${\epsilon }_2$ gilt.