Schnittwinkel zweier Ebenen

Schneiden zwei Ebenen $ε_{1} u n d ε_{2}$ einander in einer Geraden g, so bezeichnet man als Schnittwinkel $ϕ$ dieser Ebenen den Winkel zwischen denjenigen beiden Geraden, die eine dritte, zur Schnittgeraden senkrechte Ebene aus $ε_{1} u n d ε_{2}$ „herausschneidet“. Man spricht manchmal auch von dem zwischen $ε_{1} u n d ε_{2}$ liegenden „Keilwinkel“.

Schnittwinkel

#Ebenen #Schnittwinkel #Abstand #Vektoren #Normalenvektor #Ebene #Ebene im Raum #Nullvektor #Schnittpunkt #schnittfläche #Schnittgerade #parallel #orthogonal #Orthogonalität #kongruent

Schnittwinkel zweier Ebenen

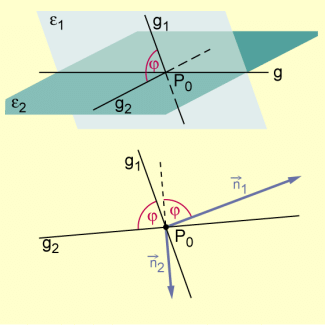
Durch diese Überlegung wird die Frage nach dem Schnittwinkel zweier Ebenen auf das einfachere Problem des Schnittwinkels zweier Geraden im Raum zurückgeführt.

Zur rechnerischen Bestimmung des Schnittwinkels betrachtet man zwei Normalenvektoren $\vec{n}_{1} u n d \vec{n}_{2}$ der Ebenen $ε_{1} u n d ε_{2}$ .

Da $\vec{n}_{1}$ senkrecht zu $ε_{1}$ und $\vec{n}_{2}$ senkrecht zu $ε_{2}$ verläuft, ist der von $\vec{n}_{1} u n d \vec{n}_{2}$ gebildete Winkel gleich dem Schnittwinkel $ϕ$ (bzw. 180° – $ϕ$ ).

Der Schnittwinkel $ϕ$ kann aus diesem Grund durch Anwendung der Definitionsgleichung für das Skalarprodukt auf die beiden Normalenvektoren $\vec{n}_{1} u n d \vec{n}_{2}$ berechnet werden.

Die Gleichungen für $\vec{n}_{1} u n d \vec{n}_{2}$ gewinnt man aus den Ebenengleichungen:

Hat die Ebene $ε$ die Gleichung $ε : \vec{x} = {\vec{p}}_{0} + r \vec{u} + s \vec{v}$ , so ist $\vec{n} = \vec{u} \times \vec{v}$ ein Normalenvektor von $ε$ . Ist die Gleichung von $ε$ in der Koordinatenschreibweise, also $a x + b y + c z + d = 0$ , angegeben, dann gilt
$\vec{n} = (\begin{matrix} a \\ b \\ c \end{matrix})$ .

Aus $\vec{n}_{1} \cdot \vec{n}_{2} = | \vec{n}_{1} | \cdot | \vec{n}_{2} | \cdot \cos ∡ (\vec{n}_{1}, \vec{n}_{2})$ erhält man
$\cos ∡ (\vec{n}_{1}, \vec{n}_{2}) = \frac{\vec{n}_{1} \cdot \vec{n}_{2}}{| \vec{n}_{1} | \cdot | \vec{n}_{2} |}$ .

Beispiel 1: Es ist der Schnittwinkel der Ebenen $ε_{1} u n d ε_{2}$ mit $ε_{1} : 2 x + y + 2 z - 8 = 0$ bzw. $ε_{2} : 6 x - 3 y + 2 z - 12 = 0$ zu bestimmen.

Aus den beiden Gleichungen kann man ablesen:
$\vec{n}_{1} = (\begin{matrix} 2 \\ 1 \\ 2 \end{matrix})$ , $\vec{n}_{2} = (\begin{matrix} 6 \\ - 3 \\ 2 \end{matrix})$

Daraus ergibt sich
$\cos ∡ (\vec{n}_{1}, \vec{n}_{2}) = \cos ϕ = \frac{(\begin{matrix} 2 \\ 1 \\ 2 \end{matrix}) \cdot (\begin{matrix} 6 \\ - 3 \\ 2 \end{matrix})}{| (\begin{matrix} 2 \\ 1 \\ 2 \end{matrix}) | \cdot | (\begin{matrix} 6 \\ - 3 \\ 2 \end{matrix}) |} = \frac{13}{3 \cdot 7} \approx 0,6190$
und damit $ϕ \approx 51,75 °$ .

(Hinweis: Ist der Winkel, der sich ergibt, größer als 90°, berechnet man den Schnittwinkel, indem man den berechneten Winkel von 180° subtrahiert.)

Beispiel 2: Durch A(6; 0; 0), B(0; 8; 0) und C(0; 0; 2) ist eine Ebene gegeben.
Es sind die Schnittwinkel dieser Ebene mit den Koordinatenebenen zu bestimmen.

Nach der Achsenabschnittsgleichung für Ebenen hat $ε$ die Gleichung $ε : \frac{x}{6} + \frac{y}{8} + \frac{z}{2} = 1$ , woraus sich $ε : 4 x + 3 y + 12 z - 24 = 0$ und damit
$\vec{n} = (\begin{matrix} 4 \\ 3 \\ 12 \end{matrix})$
für einen Normalenvektor von $ε$ ergibt.

Die Normalenvektoren der drei Koordinatenebenen sind
${\vec{n}}_{x y} = (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}), {\vec{n}}_{x z} = (\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}) u n d {\vec{n}}_{y z} = (\begin{matrix} 1 \\ 0 \\ 0 \end{matrix})$ .

Unter Verwendung der oben angegebenen Formel erhält man hieraus
$\cos ϕ_{x y} = \frac{(\begin{matrix} 4 \\ 3 \\ 12 \end{matrix}) \cdot (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix})}{| (\begin{matrix} 4 \\ 3 \\ 12 \end{matrix}) | \cdot | (\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}) |} = \frac{12}{13} \approx 0,9230 u n d d a m i t ϕ_{x y} \approx 22,62 °$ ;
$\begin{array}{l} \cos ϕ_{x z} = \frac{3}{13} u n d d a m i t ϕ_{x z} \approx 76,66 °; \\ \cos ϕ_{y z} = \frac{4}{13} u n d d a m i t ϕ_{y z} \approx 72,08 ° . \end{array}$

(Hinweis: Ist der Winkel, der sich ergibt, größer als 90°, berechnet man den Schnittwinkel, indem man den berechneten Winkel von 180° subtrahiert.)

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Schnittwinkel zweier Ebenen

Schnittwinkel

Rechtliches

Einloggen