Schnittwinkel zweier Geraden im Raum

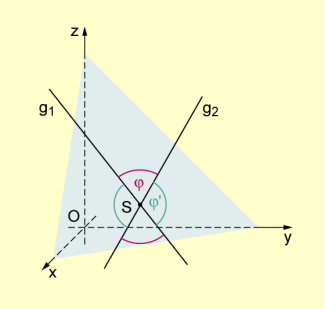
Der Schnittwinkel zweier Geraden im Raum kann demzufolge höchstens 90° betragen. In diesem Grenzfall heißen $g_{1}und{g}_2$ zueinander senkrecht bzw. orthogonal.

Um zu überprüfen, ob zwei durch ihre vektoriellen Gleichungen gegebenen Geraden $g_{1}und{g}_2$ zueinander orthogonal sind bzw. um die Gleichung einer Geraden $g_2$ zu ermitteln, die zu der gegebenen Geraden $g_1$ senkrecht ist, kann man eine Eigenschaft des Skalarprodukts zweier Vektoren verwenden:

• Zwei Vektoren $\overrightarrow{a}und\overrightarrow{b}$ sind genau dann zueinander senkrecht, wenn $\overrightarrow{a}\cdot \overrightarrow{b}=0$ gilt.

Beispiel 1: Wir betrachten im Raum die beiden Geraden $g_{1}und{g}_2$ mit den Gleichungen
$g_1:\overrightarrow{x}=\left(\begin{array}{c}0\\ 2\\ 1\end{array}\right)+t_1\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)$
bzw.
$g_2:\overrightarrow{x}=\left(\begin{array}{c}-1\\ 6\\ 5\end{array}\right)+t_2\left(\begin{array}{c}3\\ -1\\ -3\end{array}\right)$,
die einander im Punkt S(2; 5; 2) schneiden (denn für $t_1=t_2=1$ erhält man übereinstimmend
${\overrightarrow{x}}_1=\left(\begin{array}{l}2\\ 5\\ 2\end{array}\right)$).

Diese beiden Geraden sind genau dann senkrecht zueinander, wenn dies für ihre Richtungsvektoren
${\overrightarrow{a}}_{{}_1}=\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)$ und ${\overrightarrow{a}}_{{}_2}=\left(\begin{array}{c}3\\ -1\\ -3\end{array}\right)$
zutrifft. Da
$\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}3\\ -1\\ -3\end{array}\right)=2\cdot 3+3\cdot (-1)+1\cdot (-3)=0$,
sind ${\overrightarrow{a}}_{1}und{\overrightarrow{a}}_2$ sowie damit auch $g_{1}und{g}_2$ senkrecht zueinander.

Beispiel 2: Zu einer Geraden $g_1$ im Raum gibt es in jedem Punkt von $g_1$ unendlich viele Geraden, die senkrecht zu $g_1$ sind.

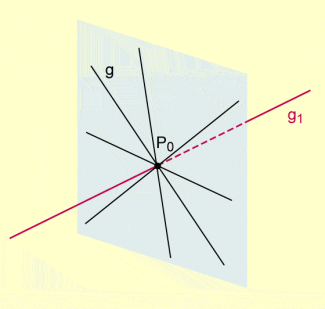
Rechnerisch findet dies folgendermaßen seinen Ausdruck:
Ist die Gerade $g_1$ beispielsweise durch
$g_1:\overrightarrow{x}=\left(\begin{array}{c}0\\ 2\\ 1\end{array}\right)+t_1\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)$
gegeben, so muss für jede Gerade g durch
${\overrightarrow{p}}_0=\left(\begin{array}{c}0\\ 2\\ 1\end{array}\right)$ mit $g:\overrightarrow{x}=\left(\begin{array}{c}0\\ 2\\ 1\end{array}\right)+t\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)$,
die senkrecht zu $g_1$ verlaufen soll, gelten:
$\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)\cdot \left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)=0$

Daraus folgt $2a_1+3a_2+a_3=0bzw.beispielsweise{a}_3=-2a_1-3a_2$.
Die Parameter $a_{1}und{a}_2$ können frei gewählt werden.
Das heißt aber: Jede Gerade g mit
$g:\overrightarrow{x}=\left(\begin{array}{c}0\\ 2\\ 1\end{array}\right)+t\left(\begin{array}{c}{a}_1\\ a_2\\ -2a_1-3a_2\end{array}\right)\left(a_1,a_2\in ℝ\right)$
verläuft in $P_0$ senkrecht zu $g_1$.

Unter Verwendung der Definitionsgleichung für das Skalarprodukt kann der Schnittwinkel zweier beliebiger (einander schneidender) Geraden $g_{1}und{g}_2$ des Raumes als Winkel zwischen den Richtungsvektoren $\overrightarrow{a}und\overrightarrow{b}$ dieser Geraden berechnet werden.

• Gilt $g_1:\overrightarrow{x}={\overrightarrow{p}}_1+t\overrightarrow{a}und{g}_2:\overrightarrow{x}={\overrightarrow{p}}_2+t\overrightarrow{b}$, so folgt wegen $\overrightarrow{a}\cdot \overrightarrow{b}=\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|\cos \psi (mit\psi =\measuredangle \left(\overrightarrow{a},\overrightarrow{b}\right))$ für den Schnittwinkel $\psi$:$\cos \psi =\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot \left|\overrightarrow{b}\right|}$

Beispiel 3: Es ist der Schnittwinkel der Geraden
$g:\overrightarrow{x}=\left(\begin{array}{c}-1\\ -1\\ -1\end{array}\right)+t\left(\begin{array}{c}2\\ 2\\ 2\end{array}\right)undh:\overrightarrow{x}=\left(\begin{array}{c}-2\\ -2\\ 0\end{array}\right)+u\left(\begin{array}{c}3\\ 3\\ 0\end{array}\right)$
(die einander im Punkt O(0; 0; 0) schneiden) zu berechnen.

Wegen $\cos \psi =\frac{\left(\begin{array}{c}2\\ 2\\ 2\end{array}\right)\cdot \left(\begin{array}{c}3\\ 3\\ 0\end{array}\right)}{\left|\left(\begin{array}{c}2\\ 2\\ 2\end{array}\right)\right|\cdot \left|\left(\begin{array}{c}3\\ 3\\ 0\end{array}\right)\right|}=\frac{12}{\sqrt{12}\cdot \sqrt{18}}=\frac{\sqrt{6}}{3}\approx \mathrm{0,8165}$ gilt $\psi \approx \mathrm{35,26}°$.