Additionstheoreme für Winkelfunktionen
Als Additionstheoreme für Winkelfunktionen werden Formeln bezeichnet, durch die die Funktionswerte von Summen und Differenzen von Winkeln auf die Werte der trigonometrischen Funktionen einzelner Winkel zurückgeführt werden.
Sinus der Summe zweier Winkel
- Für den Sinus der Summe zweier Winkel gilt:
Für Winkel zwischen und ergibt sich die Formel für den Sinus der Summe zweier Winkel mithilfe nachstehend angeführter Überlegungen am Einheitskreis.
-
Sinus der Summe zweier Winkel
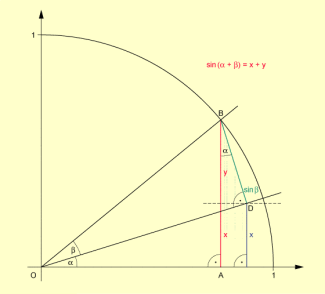
Es ist .
Aus und folgt:
Dann ist und . Für gilt somit:
bzw.
Entsprechend ergibt sich für :
bzw.
Zusammengefasst:
Für ergibt sich der Sinus des doppelten Winkels wie folgt:
Sinus der Differenz zweier Winkel
- Für den Sinus der Differenz zweier Winkel gilt:
Die Formel für den Sinus der Differenz zweier Winkel kann man anhand der folgenden Abbildung gewinnnen.
-
Sinus der Differenz zweier Winkel
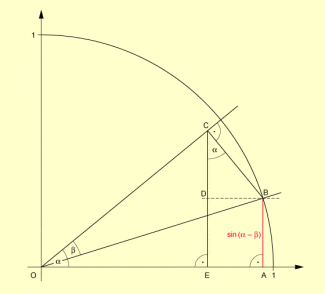
Es gilt:
Weiter ist:
bzw.
bzw.
Zusammengefasst:
Anmerkung: Man kommt zu diesem Theorem auch, wenn man in die Formel für den Sinus der Summe zweier Winkel durch ersetzt und berücksichtigt, dass und ist.
Kosinus und Tangens der Summe bzw. Differenz zweier Winkel
Für den Kosinus der Summe bzw. Differenz zweier Winkel kann man die folgende Beziehung herleiten:
Da gilt, ergibt sich für den Tangens der Summe bzw. Differenz zweier Winkel
,
was nach Kürzen durch auf die Form
führt.
Weitere Beziehungen
Aus diesen Formeln lassen sich einige weitere Beziehungen folgern, die beim Umformen trigonometrischer Ausdrücke (z.B. in goniometrischen Gleichungen) nützlich sind:
bzw.
Weiter ist:
- Beispiel aus der Elektrotechnik:
Die Beziehung erhält man durch einfache Umformungen bei Anwendung obiger Beziehungen.
In einem allgemeineren Sinn versteht man unter einem Additionstheorem eine Funktionalgleichung , wenn es für , und eine Funktion gibt, so dass und ist.

