Graphen und Eigenschaften von Winkelfunktionen
Graphen von Winkelfunktionen kann man auf die bekannte Weise unter Verwendung einer Wertetabelle zeichnen. Es ist allerdings auch möglich, ausgehend von der Definition dieser Funktionen am Einheitskreis die zu einem Winkel als Abszisse eines Graphenpunktes gehörende Ordinate sofort aus der Zeichnung zu entnehmen. Aus der Konstruktion der Funktionsgraphen lassen sich einige wichtige Eigenschaften der entsprechenden Winkelfunktionen schlussfolgern.
- Die den Ordinaten der Graphenpunkte von Sinusfunktion und Kosinusfunktion entsprechenden Strecken „wiederholen“ sich nach jeweils einem vollen „Umlauf“ des freien Winkelschenkels.
Das heißt: Die Funktionswerte, die im Abstand von aufeinanderfolgen, sind gleich.
Es gilt:
und
Sinus- und Kosinusfunktion sind also periodische Funktionen mit der Periode .
- Die Ordinaten der Graphen der Tangensfunktion (und dies gilt auch für die Kotangensfunktion) „wiederholen“ sich bereits nach jeweils einem halben „Umlauf“ des freien Winkelschenkels:
Das heißt: Die Funktionswerte, die im Abstand von aufeinanderfolgen, sind gleich. Es gilt:
und
Tangens- und Kotangensfunktion sind also periodische Funktionen mit der Periode .
- Dreht man den freien Winkelschenkel um jeweils entgegen dem Uhrzeigersinn und im Uhrzeigersinn, so unterscheiden sich die ablesbaren Sinuswerte jeweils nur im Vorzeichen, während die Kosinuswerte identisch sind.
Es gilt:
Die Sinusfunktion ist eine ungerade Funktion.
Die Kosinusfunktion ist eine gerade Funktion.
Daraus ergibt sich wegen bzw. , dass die Tangens- und die Kotangensfunktion beide ungerade sind.
-
Funktionsgraphen der Sinus-, Kosinus- und Tangensfunktion
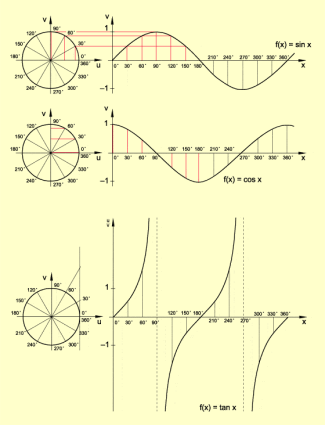
Einen Gesamtüberblick über Eigenschaften von Winkelfunktionen vermittelt die folgende Übersicht.
-
Übersicht über Eigenschaften der Winkelfunktionen
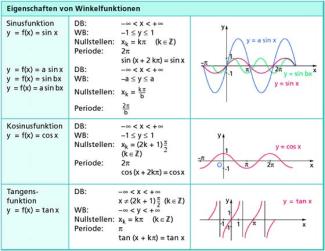
Lernhelfer (Duden Learnattack GmbH): "Graphen und Eigenschaften von Winkelfunktionen." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/graphen-und-eigenschaften-von-winkelfunktionen (Abgerufen: 11. March 2026, 20:52 UTC)

