Winkelfunktionen
Die bezüglich eines rechtwinkligen Dreiecks formulierten Definitionen des Sinus und des Kosinus (wie auch des Tangens und des Kotangens) eines Winkels können auf einen beliebigen Kreis oder speziell auch auf einen Einheitskreis (also einen Kreis mit dem Radius Längeneinheit) übertragen werden.
Bezüglich des Einheitskreises gelten folgende (zu den Definitionen an einem beliebigen Kreis äquivalente) Festlegungen:
-
Definition des Sinus und Kosinus eines Winkels am Einheitskreis
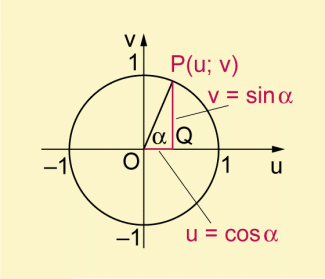
- Die Ordinate v des zum Winkel gehörenden Punktes auf dem Einheitskreis heißt Sinus des Winkels :
- Die Abszisse u des zum Winkel gehörenden Punktes auf dem Einheitskreis heißt Kosinus des Winkels :
Die Zuordnung eines Winkel zu seinem Sinus- bzw. Kosinuswert ist eindeutig, stellt also eine Funktion (hier trigonometrische Funktion oder Winkelfunktion) genannt dar.
Um zu gewährleisten, dass es sich hierbei – wie gewohnt – um eine Zahl-Zahl-Beziehung handelt, gibt man den Winkel im Bogenmaß an.
- Das Bogenmaß eines Winkels ist das Verhältnis aus der zu diesem Winkel gehörenden Kreisbogenlänge b und der Länge r des Radius des Kreises. Es wird mit (lies: arkus alpha) oder bezeichnet:
Am Einheitskreis gilt wegen eine besondere Beziehung. Als Einheit des Bogenmaßes verwendet man 1 Radiant (1 rad) und legt fest: 1 rad ist die Größe des Winkels , für den am Einheitskreis gilt.
Aus folgt in diesem Falle .
Mit anderen Worten: Der Winkel im Gradmaß hat das Bogenmaß .
Auf die Angabe der Einheit rad wird häufig verzichtet.
![]()
Beispiel:
Häufig werden die in der folgenden Tabelle zusammengestellten Werte benutzt.
| Gradmaß | ||||||||
| Bogenmaß | 0 |
Geht man außerdem von der Auffassung aus, dass der zweite Schenkel des Winkels beliebig oft und zudem im mathematisch positiven wie im mathematisch negativen Drehsinn um den Ursprung gedreht werden kann, so lässt sich der Winkelbegriff erweitern:
Jede hinzukommende volle Umdrehung verändert den Winkel um (bei Drehung im bzw. entgegen dem Uhrzeigersinn). Als Definitionsbereich für die oben genannten Funktionen kann damit die gesamte Menge der reellen Zahlen verwendet werden.
Anmerkung: Der Übergang zur Winkelmessung in Bogenmaß soll nachfolgend durch die Verwendung von x als Winkelbezeichnung kenntlich gemacht werden.
- Die eindeutige Zuordnung nennt man Sinusfunktion, die eindeutige Zuordnung Kosinusfunktion.
Die folgende Tabelle gibt Beispiele von Funktionswerten der Sinus- bzw. Kosinusfunktion an.
| x | 0 | |||||||
| sin x | 1 | 0 | -1 | 0 | 1 | 0 | -1 | 0 |
| cos x | 0 | -1 | 0 | 1 | 0 | -1 | 0 | 1 |
Die Definition des Tangens eines Winkels x kann sofort unter Verwendung des Sinus und des Kosinus dieses Winkels, aber auch mit Bezug auf den Einheitskreis und der Tangente an diesen im Punkt erfolgen:
-
Definition des Tangens eines Winkels am Einheitskreis
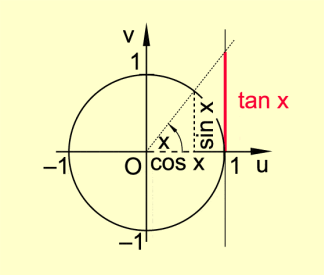
Für beliebige Winkel x heißt der Quotient aus dem Sinus und dem Kosinus dieses Winkels Tangens des Winkels x.
Die eindeutige Zuordnung nennt man Tangensfunktion.
Entsprechend heißt der Quotient aus dem Sinus eines Winkels x der Kotangens von x und die eindeutige Zuordnung die Kotangensfunktion.

