Anwendungen von Differenzengleichungen

Ratensparen, Guthabenverrentung und Annuitätendarlehen

Ein Konto hat einen Stand $K\left(K>\mathrm{0...}Guthaben,\text{ K}<\text{0}\mathrm{...}\text{ Darlehen}\right)$, der sich durch Zinsen und Einzahlungen bzw. Abhebungen mit der Zeit ändert; es gilt also $K=K\left(t\right)$. Der Verzinsungszeitraum sei $\Delta t=1Jahr$. Die Zinsen werden jeweils am Jahresende auf dem Konto verbucht. Ebenfalls am Jahresende wird eine Rate r auf das Konto eingezahlt $\left(r>0\right)$ oder dem Konto entnommen $\left(r<0\right)$. Weitere Buchungen gibt es auf dem Konto nicht.

Die Änderung $\Delta K$ des Kontostandes K kommt also durch die Rate r und durch die Zinsen $Z=p\cdot K$ bei einem Jahreszinssatz p zustande. Es gilt:
$\Delta K=p\cdot K+r\text{ oder K}\left(\text{t+}\Delta \text{t}\right)=\left(1+p\right)K\left(t\right)+r{\text{ oder K}}_{\text{i}\text{+1}}=\left(1+p\right)K_i+r$

Der letzte Ausdruck ist eine lineare inhomogene Differenzengleichung 1. Ordnung der Form $y_{i+1}=a\cdot y_i+b$, wobei $K_i$ dem $y_i$ entspricht sowie $a=1+p\text{ bzw}\text{. b}=r$ gilt.
Der Kontostand nach dem i-ten Verzinsungszeitraum ergibt sich mit $a=1+p\ne 1$ zu:
$K_i=c\cdot {\left(1+p\right)}^i-\frac{r}{1+p-1}=c\cdot {\left(1+p\right)}^i-\frac{r}{p}$

Am Anfang $\left(i=0\right)$ beträgt der Kontostand $K_0\left(K_0>\mathrm{0...}\text{ Guthabeneinlage}{\text{, K}}_{\text{0}}<\mathrm{0...}\text{ Darlehnssumme}\right)$,
woraus sich der Parameter c bestimmen lässt:
$K_0=c{\left(1+p\right)}^0-\frac{r}{p}=c-\frac{r}{p},\text{ also c}=K_0+\frac{r}{p}$

Die partikuläre Lösung lautet somit:
$K_i=\left(K_0+\frac{r}{p}\right)\cdot {\left(1+p\right)}^i-\frac{r}{p}$ bzw. $K_i=K_0\cdot {\left(1+p\right)}^i+\frac{r}{p}\cdot \left({\left(1+p\right)}^i-1\right)$

Die erhaltene Gleichung bezeichnet man als nachschüssige Rentenformel.

Mit dem mathematisch beschriebenen Sachverhalt werden mehrere reale Vorgänge erfasst:

1. Guthabenverzinsung
   Auf einem Konto befindet sich ein Guthaben, das im Zeitraum $\Delta t$bestimmte Zinsen erbringt.
   Im folgenden Zeitraum wird das Guthaben einschließlich der Zinsen verzinst $\left(K_0>0,\text{ r}=0\right)$.
    
2. Ratensparen
   Auf einem Konto befindet sich ein Guthaben, das im Zeitraum $\Delta t$verzinst wird.
   Zusätzlich wird am Ende jedes Verzinsungszeitraumes ein fester Betrag eingezahlt $\left(K_0>0,\text{ r}>0\right)$.
    
3. Guthabenverrentung
   Auf einem Konto befindet sich ein Guthaben, das im Zeitraum $\Delta t$ verzinst wird.
   Am Ende jedes Verzinsungszeitraumes wird ein fester Betrag $\left(K_0>0,\text{ r}<0\right)$ abgehoben.
    
4. Annuitätendarlehen
   Ein Darlehen eines Bankkunden wird auf einem Konto geführt. Am Ende jedes Verzinsungszeitraums zahlt er einen festen Betrag – die Annuität – auf das Konto ein, um die Zinsen zu zahlen und das Darlehen zu tilgen. Da der Kunde den Kontostand und die anfallenden Zinsen der Bank schuldet, gehen Kontostand sowie Zinsen mit negativem Vorzeichen in die Rechnung ein $\left(K_0<0,\text{ r}>0\right)$.

Die verschiedenen Fälle sind in der folgenden Abbildung für bestimmte Parameter gegenübergestellt.

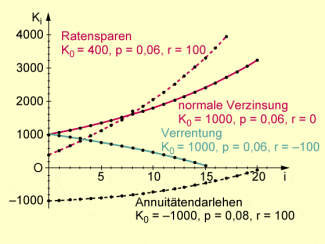
Für den Fall des Annuitätendarlehens ist die Berechnung des Kontostandes, der Zinsen und der Tilgung in nachstehender Tabelle aufgeführt.

In der Tabelle kann der Kontostand $K_i$ im i-ten Jahr ausgehend von $K_0$ nach der Differenzengleichung oder der nachschüssigen Rentenformel berechnet werden.
Die Zinsen am Ende des i-ten Jahres ergeben sich aus $Z_i=p{\text{ K}}_{\text{i}}$.
Die Kontostandsänderung $\Delta {\text{K}}_{\text{i}}$ ist die Summe der Zinsen und der Rate, kann aber auch als ${\text{K}}_{\text{i}\text{+1}}-K_i$ berechnet werden.

Temperaturanpassung an Umgebungstemperatur

Befindet sich ein Körper mit der Temperatur T in einer Umgebung der Temperatur ${\text{T}}_{\text{u}}$, so wird sich seine Temperatur in Richtung der Umgebungstemperatur so lange ändern, bis ein Temperaturausgleich erfolgt ist. Dabei wird in einer Zeiteinheit $\Delta t$ die Temperaturänderung $\Delta \text{T}$ umso größer sein, je größer der Unterschied der Temperaturen T und ${\text{T}}_{\text{u}}$ ist.

Es gilt $\Delta \text{T}\sim {\text{T}}_{\text{u}}\sim T\left(newtonsches\text{ Abkühlungsgesetz}\right)$, also auch
$\Delta \text{T}=k\left({\text{T}}_{\text{u}}-T\right)\text{ bzw}\text{. T}\left(t+\Delta t\right)=k{T}_u+\left(1-k\right)T\left(t\right)$ oder $T_{i+1}=\left(1-k\right)T_i+k{T}_u,\text{ i}\in \mathbb{N}$, wobei k ein auf das Zeitintervall $\Delta t$ bezogener Temperaturkoeffizient ist, der die Geschwindigkeit des Temperaturausgleichs charakterisiert.

Das newtonsche Abkühlungsgesetz entspricht der linearen homogenen Differenzengleichung $y_{i+1}=a\cdot y_i+b$.
Dem $T_i$ entspricht $y_i$ und es gilt $a=1-k$ und $b=k{T}_u$.

Da $k\ne 0$ und damit $a\ne 1$ vorausgesetzt werden kann, ist folgende Funktion Lösung der Differenzengleichung:
$T_i=c{\left(1-k\right)}^i-\frac{k{T}_u}{l-k-l}=c{\left(1-k\right)}^i+T_u,{\text{ also T}}_{\text{i}}=c{\left(1-k\right)}^i+T_u,\text{ c}\in ℝ$

Ist zur Zeit $t_0=0$ die Temperatur des Körpers $T=T_0$, so kann c bestimmt werden:
$T_0=c{\left(1-k\right)}^0+T_u,\text{ also }c=T_0-T_u$ und damit $T_i=T_u+\left(T_0-T_u\right){\left(1-k\right)}^i$

Sind k, $T_0$ und ${\text{T}}_{\text{u}}$ für einen Körper bekannt, so kann nach der erhaltenen Gleichung die Temperatur $T_i$ dieses Körpers zu allen Zeiten $t=t_0+i\Delta t$ berechnet werden. Der umgekehrte Weg ist jedoch auch möglich und praktisch wichtig, um den Temperaturkoeffizienten k eines Körpers oder die Umgebungstemperatur ${\text{T}}_{\text{u}}$ zu bestimmen. Dazu muss eine Folge von Messwerten $T_i$ mit konstantem Zeitabstand zwischen den einzelnen Messungen vorliegen.

Beispiel

Ein Becherglas wird mit Leitungswasser gefüllt und in ein Wasser-Eis-Gemisch getaucht, in dem ein Magnetrührer arbeitet. Über einen Temperaturfühler wird im Abstand von $\Delta t$ die Temperatur aufgezeichnet. In einem solchen Experiment mit einem 50-ml-Becherglas, $T_u={\mathrm{2,8}}^{\circ }C\text{ und }\Delta t=60s$ ergaben sich die in Tabelle 1 enthaltenen Messwerte. Tabelle 2 enthält die Werte für das $T_{i+1}/T_i\text{-Diagramm}$.

Das $T_{i+1}/T_i\text{-Diagramm}$ bestätigt, dass die Messwerte $T_i$ einer linearen Differenzengleichung gehorchen. Für die Gerade durch die Messpunkte müssen nun Anstieg und Verschiebung berechnet werden, um die Parameter der Gleichung $T_{i+1}=\left(1-k\right)T_i+k{T}_u$ bestimmen zu können:

Anstieg (berechnet aus erstem und letztem Punkt in Tabelle 2):
$1-k=\frac{{\mathrm{4,6}}^{\circ }C-{\mathrm{6,0}}^{\circ }C}{{\mathrm{5,2}}^{\circ }C-{\mathrm{7,1}}^{\circ }C}=\frac{-{\mathrm{1,4}}^{\circ }C}{-{\mathrm{1,9}}^{\circ }C}=\mathrm{0,7368}$, also $k=\mathrm{0,2632}$
Verschiebung (berechnet aus dem erstem Punkt in Tab. 3):
$k{T}_u={\mathrm{6,0}}^{\circ }C-\frac{\mathrm{1,4}}{\mathrm{1,9}}\cdot {\mathrm{7,1}}^{\circ }C=\mathrm{0,7684}$, also $T_u={\mathrm{2,9}}^{\circ }C$
Als die an die Messpunkte angepasste Lösung der Differenzengleichung erhält man somit $T_i={\mathrm{2,9}}^{\circ }C+{\mathrm{4,2}}^{\circ }C\cdot {\mathrm{0,7368}}^i$.

Die Abkühlkurve zeigt sowohl die Messdaten als auch die über die gefundene Differenzengleichung ermittelten Werte. Die kleinen Abweichungen sind durch Messfehler bedingt.