Bereichsintegrale

In der xy-Ebene eines rechtwinkligen xyz-Koordinatensystems sei ein beliebiger, jedoch beschränkter Bereich G gegeben, der messbar ist (hier zu verstehen als: dessen Inhalt bestimmbar ist).
Für diesen Bereich sei eine beschränkte Funktion f mit $z=f\left(x,y\right)$ erklärt, von der zunächst angenommen wird, dass sie in G nicht negativ ist.
Es werde dann mit K diejenige räumliche Punktmenge bezeichnet, für deren Punkte $\left(x;y;z\right)$

1. der in der xy-Ebene liegende Punkt mit den Koordinaten (x; y) zu G gehört und
2. $0\le z\le f\left(x,y\right)$ ist.

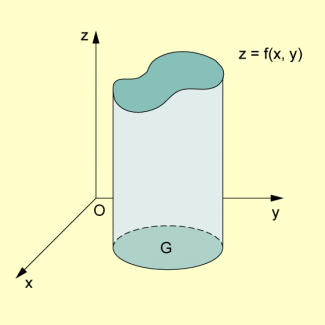
Dieser räumliche Bereich K besitzt ein Volumen, das man mithilfe des entsprechenden Bereichsintegrals berechnen kann.

Bereichsintegral nennt man ein Integral einer Funktion mehrerer Variabler, wobei der Integrationsbereich eine beschränkte und messbare Teilmenge des Variablengrundbereichs ist.

Das Integral der Funktion $z=f\left(x,y\right)$ über dem Gebiet G schreibt man in der Form ${\displaystyle \underset{G}{\int }f\left(x,y\right)dxdy}$.

Es gilt dann also V = ${\displaystyle \underset{G}{\int }f\left(x,y\right)dxdy}$.

Bereichsintegrale können häufig auf zweifache Integrale zurückgeführt werden, wenn zusätzlich der Begriff eines Normalbereichs (eines rechteckigen [xy-]Bereichs) eingeführt wird.