Berechnung der Bogenlänge

Die Berechnung der Bogenlänge ist für die Bearbeitung innermathematischer und vieler technischer (insbesondere bautechnischer) Probleme bedeutsam.
Als Beispiele seien die Berechnung der Länge eines Parabelbogens, der Kettenlinie, einer Schleife oder eines Brückenbogens genannt.

Eine Kurve sei in einem Intervall $[a; b]$ als Graph einer Funktion f mit der Gleichung $y = f (x)$ gegeben.

Bogen zwischen zwei Punkten einer Kurve

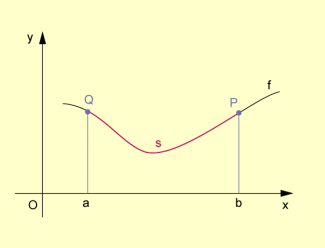
Die Berechnung der Länge s des Kurvenbogens zwischen den Punkten P und Q kann dann unter Verwendung nachstehenden Satzes erfolgen:

Ist f eine über einem Intervall $[a; b]$ differenzierbare Funktion, dann besitzt der Bogen des Graphen von f im Intervall $[a; b]$ die Länge
$s = \int_{a}^{b} \sqrt{1 + y'^{2}} d x = \int_{a}^{b} \sqrt{1 + {[f' (x)]}^{2}} d x$ .

Beispiele für innermathematische und praktische Anwendungen

(1) Wie lang ist der Parabelbogen, der im ersten Quadranten von der Parabel $y = \sqrt{x}$ im Intervall $[0; 16]$ gebildet wird?

Parabelbogen

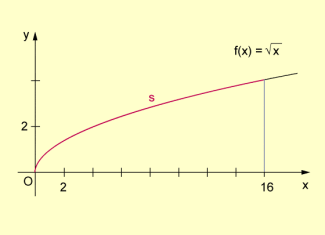
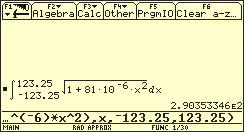
Mit $y' = \frac{1}{2 \sqrt{x}}$ ergibt sich für die Berechnung der Bogenlänge das Integral $s = \int_{0}^{16} \sqrt{1 + \frac{1}{4 x}} d x$ .

Setzt man für die Berechnung dieses komplizierten Integrals einen Rechner mit CAS ein, so ergibt sich (als überspringbares Zwischenergebnis) zunächst für das unbestimmte Integral
$\int \sqrt{1 + \frac{1}{4 x}} d x = - \frac{1}{8} (\ln | x | + 2 (\ln (\sqrt{\frac{4 x + 1}{x}} - 2) - 2 x \sqrt{\frac{4 x + 1}{x}}))$
und daraus dann als Wert für die Bogenlänge $s \approx 16,82 (L E)$ .

Berechnung der Parabelbogenlänge mit GTR

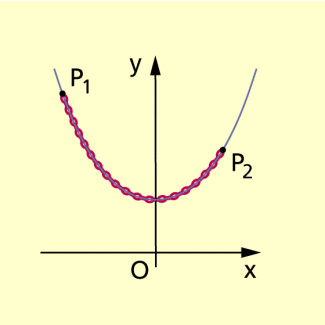
(2) Der Graph der Funktion f mit $y = f (x) = \frac{1}{2} (e^{x} + e^{- x})$ heißt Kettenlinie.
Die Länge der Kettenlinie soll im Intervall $[- a; a]$ berechnet werden.

Kettenlinie

Aus $y = f (x) = \frac{1}{2} (e^{x} + e^{- x})$ folgt
Bild .
Für die Bogenlänge ergibt sich dann:
Bild
Wegen der Achsensymmetrie gilt:
Bild

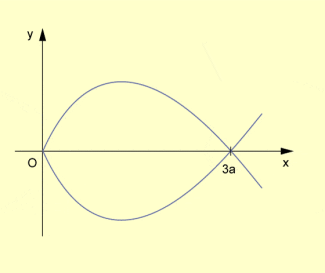
(3) Die im Folgenden abgebildete Kurve (eine Schleife) ist der Graph der Funktion mit der Gleichung
$9 a y^{2} = x {(x - 3 a)}^{2} (a > 0, x \geq 0)$ .
Die Länge der Schleife soll berechnet werden.

Schleife

Es ist
Bild

Daraus folgt $y' = \frac{a - x}{2 \sqrt{a x}}$ .
Damit gilt:
$\begin{matrix} s = 2 \cdot \int_{0}^{3 a} \sqrt{1 + \frac{{(a - x)}^{2}}{4 a x}} d x = 2 \cdot \int_{0}^{3 a} \sqrt{\frac{{(a + x)}^{2}}{4 a x}} d x \\ = 2 \cdot \int_{0}^{3 a} \frac{a + x}{2 \sqrt{a x}} d x \\ = {[\frac{2}{3} \sqrt{\frac{x}{a}} \cdot (x + 3 a)]}_{0}^{3 a} = 4 \sqrt{3} \cdot a (L E) \end{matrix}$

(4) Das Verkehrsprojekt Deutsche Einheit umfasst den Bau einer Autobahn durch den Thüringer Wald, die dessen Kamm von Ilmenau nach Zella-Mehlis quert. Unmittelbar vor dem Rennsteigtunnel als der Hauptkammdurchquerung wird die Autobahn durch die größte Bogenbrücke Deutschlands über das Tal der Wilden Gera geführt.
Die Bogenspannweite beträgt 252 m (Bauwerksgesamtlänge 552 m), wobei im Bogenbereich sechs Pfeiler im Abstand von jeweils 42 m die Fahrbahn tragen.

Bild

Die Brücke erhebt sich etwa 110 m über dem Talgrund, der Beginn des Bogens und der Fußpunkt der äußersten Pfeiler liege rund 38,5 m über dem Talgrund. Die Stärke des Bogens verringert sich von 5,5 m an den Widerlagern auf 3,3 m im höchsten Punkt. Man berechne näherungsweise die Länge des inneren Bogens.

Bild

Zur Lösung dieser Aufgabe nehmen wir an, dass der innere Brückenbogen durch den Graphen einer quadratischen Funktion angenähert werden kann.
Die innere Parabel hat (unter Berücksichtigung der Bogenstärke) dann den Scheitelpunkt $S (0; - 3,3)$ und geht durch die Punkte $P_{1; 2} (\pm 123,25; - 71,5)$ .
Unter Beachtung der Achsensymmetrie erhält man aus $y = a x^{2} + c$ als Gleichung der Parabel $y = - 0,0045 x^{2} - 3,3$ .
Mit $y' = - 0,009 x$ folgt für die Bogenlänge
$s = \int_{- 123,25}^{123,25} \sqrt{1 + {(- 0,009 x)}^{2}} d x \approx 290 (m)$ .