Schwerpunkt einer Fläche

Greift an einem starren und um eine Achse drehbaren Körper eine Kraft $\overrightarrow{F}$ an, so wirkt ein Drehmoment M. und es gilt $M=F\cdot a.$

Dabei ist a der Abstand der Wirkungslinie der Kraft von der Drehachse, auch „Hebelarm“ genannt, und F der Betrag der Kraft $\overrightarrow{F.}$

Denkt man sich nun eine Fläche, die gleichmäßig mit Masse belegt ist, in kleine Massenelemente aufgeteilt, so greift an jedem Massenelement m die Gewichtskraft an. Dadurch entsteht ein Drehmoment bezüglich einer beliebigen Drehachse.

Bezeichnet man die auf die Fläche bezogene Massedichte mit $\mu ,$ die Erdbeschleunigung mit g und die Größe des einzelnen Flächenelements mit $\Delta A,$ so gilt für das Massenelement $\Delta m$
$\Delta m=\mu \cdot \Delta A$ und für die auf dieses Massenelement wirkende Gewichtskraft $g\cdot \Delta m=g\cdot \mu \cdot \Delta A.$
Für den auf das Massenelement $\Delta m$ entfallenden Anteil $\Delta M$ des Gesamtdrehmoments folgt dann $\Delta M=g\cdot \mu \cdot \Delta A\cdot a.$

Nun gibt es zu einer Fläche (einem Körper) genau einen Punkt S, der durch folgende Eigenschaft gekennzeichnet ist:
Legt man durch S eine beliebige Achse, so hat die Summe der Drehmomente aller Massenelemente der Fläche (des Körpers) bezüglich dieser Achse die Maßzahl 0.
Dieser Punkt wird als „Schwerpunkt“ bezeichnet. Seine Lage (seine Koordinaten) zu kennen, ist wichtig für das Lösen vieler physikalischer und technischer Probleme.

Die zu untersuchende Fläche ist in der folgenden Abbildung dargestellt.

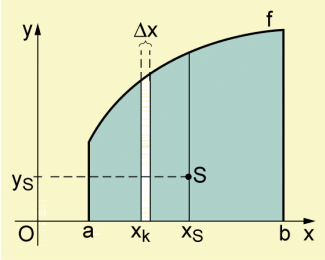
Der Inhalt dieser Fläche hat dann die Maßzahl
$A={\displaystyle {\int }_a^{b}f(x)dx}.$

Zur Ermittlung der Koordinaten $x_{s}und{y}_s$ des Schwerpunktes wird durch S eine zur y-Achse parallele Achse gelegt. Dann besitzen alle Massenelemente, die auf einem schmalen, zur y-Achse parallelen Streifen der Breite $\Delta x$ liegen, nahezu das gleiche Drehmoment bezüglich der gewählten Schwerelinie. Der Streifen hat die Flächenmaßzahl $f(x_k)\cdot \Delta x.$
Für das Drehmoment des Streifens gilt:
$\Delta M_k\approx g\cdot \mu \cdot f(x_k)\cdot \Delta x\cdot (x_s-x_k)$

Um das Gesamtdrehmoment zu ermitteln, ist nun die Summe der Drehmomente aller Streifen der Fläche zu bilden und der Grenzwert dieser Summe für $\Delta x\to 0$ zu berechnen.
Es ergibt sich so das folgende Integral:
$\underset{n\to \infty }{\lim }{\displaystyle \sum _{k=1}^n\Delta M_k}={\displaystyle {\int }_a^{b}g\cdot \mu \cdot f(x)\cdot (x_s-x)dx}$

Da die Achse durch den Schwerpunkt gehen soll, ist dieses Integral gleich null.

Wegen $g,\mu \ne 0$ gilt $x_s\cdot {\displaystyle {\int }_a^{b}f(x)dx}-{\displaystyle {\int }_a^{b}x\cdot f(x)dx}=\mathrm{0,}$ woraus folgt:
$x_s=\frac{{\displaystyle {\int }_a^{b}x\cdot f(x)dx}}{{\displaystyle {\int }_a^{b}f(x)dx}}$

Durch analoge Überlegungen ergibt sich:
$y_s=\frac{\frac{1}{2}\cdot {\displaystyle {\int }_a^b{\left[f(x)\right]}^{2}dx}}{{\displaystyle {\int }_a^{b}f(x)dx}}$

Beispiel: Es ist der Schwerpunkt der im Folgenden abgebildeten Dreiecksfläche zu ermitteln.

$\begin{array}{l}A={\displaystyle {\int }_0^{2}f(x)dx={\displaystyle {\int }_a^b(-\frac{x}{2}+1)dx}}=1\\ {\displaystyle {\int }_0^{2}x\cdot f(x)dx}={\displaystyle {\int }_0^2(-\frac{x^2}{2}+x)dx}={\left[-\frac{x^3}{6}+\frac{x^2}{2}\right]}_0^2=-\frac{4}{3}+2=\frac{2}{3}\\ {\displaystyle {\int }_0^2{\left[f(x)\right]}^{2}dx}={\displaystyle {\int }_0^2(\frac{x^2}{4}-x+1)dx}={\left[\frac{x^3}{12}-\frac{x^2}{2}+x\right]}_0^2=\frac{2}{3}-2+2=\frac{2}{3}\end{array}$
Somit ist $x_s=\frac{\frac{2}{3}}{1}=\frac{2}{3}$ und $y_s=\frac{\frac{1}{2}\cdot \frac{2}{3}}{1}=\frac{1}{3}$.