Numerische Integration

Sind Funktionen nicht elementar integrierbar oder ist das Ermitteln von Stammfunktionen zu aufwendig, werden numerische Integrationsverfahren zur näherungsweisen Berechnung bestimmter Integrale eingesetzt.
Derartige Methoden bilden auch den Hintergrund für die Integration durch elektronische Rechner (sofern die Integration hierbei nicht über ein Computeralgebrasystem realisiert wird).
Um den Flächeninhalt unter dem Graphen – und damit das bestimmte Integral – einer Funktion f in einem Intervall [a; b] näherungsweise zu bestimmen, wird die Fläche durch Parallelen zur y-Achse in gleichbreite Streifen mit leicht berechenbarem Inhalt zerlegt. Die Summe der Flächeninhalte ergibt dann einen Näherungswert für das bestimmte Integral im Intervall [a; b]. Eine derartige angenäherte zahlenmäßige Berechnung eines bestimmten Integrals heißt numerische Integration.

Die geometrische Deutung des bestimmten Integrals besagt, dass das bestimmte Integral
$\int_{a}^{b} f (x) d x$
diejenige positive Zahl ist, die den Inhalt A der Fläche angibt, welche vom Graphen der Funktion f , der x-Achse sowie den Geraden x = a und x = b begrenzt wird.
Es gilt also
$A = \int_{a}^{b} f (x) d x$ .

Bild

Vorausgesetzt sei, dass f eine im Intervall [a; b] definierte und dort nichtnegative Funktion sei, die in jedem abgeschlossenen Teilintervall von [a; b] einen kleinsten und einen größten Funktionswert besitzt.

Um den Flächeninhalt unter dem Graphen – und damit das bestimmte Integral – einer Funktion f in einem Intervall [a; b] näherungsweise zu bestimmen, wird die Fläche durch Parallelen zur y-Achse in gleichbreite Streifen mit leicht berechenbarem Inhalt zerlegt. Die Summe der Flächeninhalte ergibt dann einen Näherungswert für das bestimmte Integral im Intervall [a; b]. Eine derartige angenäherte zahlenmäßige Berechnung eines bestimmten Integrals heißt numerische Integration.

Bild

Die zur Definition des bestimmten Integrals verwendeten Ober- und Untersummen (interaktives Beispiel 1) bilden eine erste Näherung für das bestimmte Integral:
Untersumme: $\int_{a}^{b} f (x) d x \approx \sum_{i = 1}^{n} f ({\underline{x}}_{i}) \cdot Δ x$
Obersumme: $\int_{a}^{b} f (x) d x \approx \sum_{i = 1}^{n} f ({\bar{x}}_{i}) \cdot Δ x$

Die Güte der Näherung wird dadurch bestimmt, wie genau sich das obere Ende des Streifens dem Funktionsverlauf anpassen lässt, wie gut also die Streifenfläche mit der Fläche unter dem Graphen im betrachteten Intervall zur Übereinstimmung gebracht werden kann.
Das hängt zum einen von der Anzahl der Teilintervalle ab, denn je größer die Anzahl der verwendeten Streifen (je kleiner also die Streifenbreite) gewählt wird, umso besser nähert man sich dem eigentlichen Wert an.

Zerlegung einer zu berechnenden Fläche in n Teilflächen

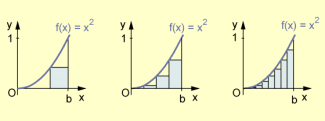
Zum anderen wird die Fläche unter der Kurve in der Regel von parabelförmig begrenzten Streifen (simpsonsche Regel, keplersche Fassregel) besser ausgefüllt als von Rechtecken (Rechteckmethode) oder Trapezen (Trapezmethode).

Die Trapezmethode soll im Folgenden ausführlicher betrachtet werden.

Trapezmethode: Die zu berechnende Fläche wird durch n Trapeze angenähert.

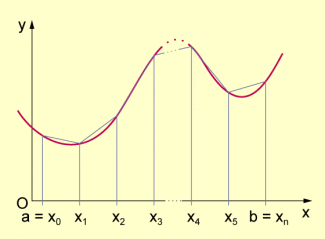
Hierbei bilden die Schnittpunkte der Parallelen mit dem Graphen von f und mit der x-Achse die Eckpunkte von Trapezen, welche die Teilflächen annähern. Die Höhe der Trapeze ist gleich der Breite $Δ x$ der Teilflächen. Sie ergibt sich aus dem betrachteten Intervall [a; b] und der Anzahl der Teilungen n. Es gilt $Δ x = \frac{b - a}{n} .$

Die Länge der beiden Grundseiten eines Trapezes entspricht den Funktionswerten $f (x_{n}) u n d f (x_{n - 1})$ und $f (x_{n}) u n d f (x_{n - 1})$ an den Rändern des jeweiligen Teilintervalls. Voraussetzung ist auch hier, dass f im betrachteten Intervall stetig und nicht negativ ist.

Bild

Der Flächeninhalt eines einzelnen Trapezes ist:
$A_{n} = Δ x \cdot \frac{f (x_{n - 1}) + f (x_{n})}{2} m i t Δ x = \frac{b - a}{n .}$

Die Summe aller Trapeze und damit den Näherungswert für das gesuchte Integral über dem Intervall [a; b] ist dann:
$S_{n} = A_{1} + A_{2} + A_{3} + \dots + A_{n}$

Beispiel

Näherungsweises Berechnen des bestimmten Integrals
$\int_{- 1}^{1} \sqrt{1 - x^{2}} d x$
(Flächeninhalt eines Halbkreises mit r = 1 LE) mittels Rechteckmethode, Trapezmethode und simpsonscher Regel für n = 10 und $Δ x = 0,2.$

Wertetabelle:
Bild

Bild

Der exakte Wert des bestimmten Integrals beträgt $\frac{π}{2} \approx 1,571$ . Die Abweichung der ermittelten Näherungen liegt zwischen etwa 0,05 bei den ersten beiden Methoden und 0,02 bei der simpsonschen Regel. Diese liefert wegen des höheren theoretischen Aufwandes normalerweise immer genauere Näherungen. Die Trapezmethode führt hier zu keinem besseren Ergebnis als die schlichtere Rechteckmethode, da die wichtigen Werte am Rand beide gleich null sind.

Unter Verwendung von Computer- oder Taschenrechnerprogrammen ist der Arbeitsaufwand auch bei einer größeren Anzahl von Teilintervallen und einer damit verbundenen hohen Genauigkeit unerheblich.

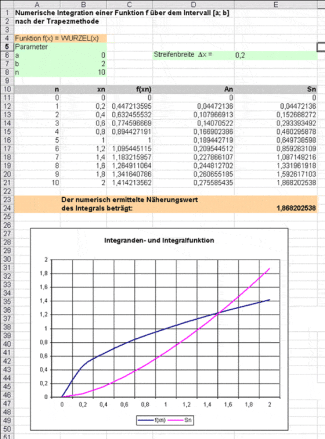
Die Berechnung der einzelnen Flächeninhalte $A_{n}$ (Trapeze) und der Summe $S_{n}$ kann mithilfe einer Tabellenkalkulation, wie zum Beispiel mit dem Kalkulationsprogramm MS Excel, durchgeführt werden.

Es wird die Funktion $f (x) = \sqrt{x}$ über dem Intervall [0; 2] numerisch integriert. Gesucht ist also ein Näherungswert für das bestimmte Integral
$\int_{0}^{2} \sqrt{x} d x$ .

Numerische Integration mithilfe einer Tabellenkalkulation

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Angaben zum Lexikon

Impressum

Numerische Integration

Beispiel

Rechtliches

Einloggen