Flächeninhalt eines Dreiecks

Aus der Elementargeometrie ist die folgende Formel für den Flächeninhalt des Dreiecks bekannt:
$A = \frac{g \cdot h}{2}$

Für die analytische Geometrie sollen nun eine Formel in Koordinatendarstellung und eine in Vektordarstellung entwickelt werden.

Umfang und Flächeninhalt von Dreiecken

#Dreieck #Umfang #Flächeninhalt #Flächenberechnung

Aufgaben und Übungen zum Flächeninhalt von Dreiecken gibt es hier!

Koordinatendarstellung

Die Fläche $A_{D}$ des Dreiecks ABC kann folgendermaßen aus Parallelogrammen gebildet werden:
$\begin{array}{l} A_{D} = A_{A A' C' C} + A_{C C' B B} + A_{A A' B' B} \\ = A_{1} + A_{2} - A_{3} (*) \end{array}$

Dreieck im ebenen kartesischen Koordinatensystem

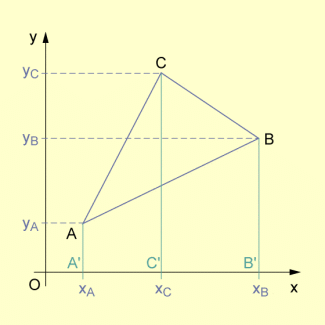
Für die Flächeninhalte der entsprechenden Trapeze $A A' C' C, C C' B B u n d A A' B' B$ gilt:
$\begin{array}{l} A_{1} = \frac{y_{C} + y_{A}}{2} (x_{C} - x_{A}) \\ A_{2} = \frac{y_{B} + y_{C}}{2} (x_{B} - x_{C}) \\ A_{3} = \frac{y_{B} + y_{A}}{2} (x_{B} - x_{A}) \end{array}$

In die Gleichung $(*)$ eingesetzt liefert dies
$A_{D} = \frac{1}{2} [(y_{C} + y_{A}) (x_{C} - x_{A}) + (y_{B} + y_{C}) (x_{B} - x_{C}) - (y_{B} + y_{A}) (x_{B} - x_{A})]$
bzw. (ausmultipliziert)
$A_{D} = \frac{1}{2} [(y_{A} x_{C} - y_{C} x_{A}) + (y_{C} x_{B} - y_{B} x_{C}) + (y_{B} x_{A} - y_{A} x_{B})]$
oder (vereinfacht)
$A_{D} = \frac{1}{2} [x_{A} (y_{B} - y_{C}) + x_{B} (y_{C} - y_{A}) + x_{C} (y_{A} - y_{B})] .$

Sind die Koordinaten der Eckpunkte eines Dreiecks ABC gegeben, so lässt sich sein Flächeninhalt folgendermaßen berechnen:
$A_{D} = \frac{1}{2} [x_{A} (y_{B} - y_{C}) + x_{B} (y_{C} - y_{A}) + x_{C} (y_{A} - y_{B})]$

Auch vektoriell lässt sich der Flächeninhalt ermitteln.

Wird das Dreieck ABC durch die Vektoren $\vec{c} = \vec{A B} u n d \vec{b} = \vec{A C}$ aufgespannt, dann gilt:
$A = \frac{1}{2} | \vec{b} \times \vec{c} |$

In Determinantenform geschrieben ergibt sich schließlich:
$A_{D} = \frac{1}{2} | \begin{matrix} x_{B} - x_{A} & y_{B} - y_{A} \\ x_{C} - x_{A} & y_{C} - y_{A} \end{matrix} |$

Beispiel 1: Es ist der Flächeninhalt des Dreiecks ABC mit $A (- 2; 11), B (10; 6) u n d C (- 6; 8)$ zu berechnen.

Einsetzen in die oben entwickelte Formel ergibt:
$\begin{array}{l} A_{D} = \frac{1}{2} \cdot [- 2 \cdot (6 + 8) + 10 \cdot (- 8 - 11) - 6 \cdot (11 - 6)] \\ A_{D} = \frac{1}{2} \cdot [- 2 \cdot 14 + 10 \cdot (- 19) - 6 \cdot 5] = - 124 \end{array}$

Das gleiche Ergebnis liefert die Berechnung mithilfe der Determinante:
$\begin{array}{l} A_{D} = \frac{1}{2} | \begin{matrix} 10 + 2 & 6 - 11 \\ - 6 + 2 & - 8 - 11 \end{matrix} | = \frac{1}{2} | \begin{matrix} 12 & - 5 \\ - 4 & - 19 \end{matrix} | \\ = \frac{1}{2} \cdot (- 228 - 20) = - 124 \end{array}$

Da dieses Dreieck, wie man leicht in einer Skizze sieht, im mathematisch negativen Drehsinn durchlaufen wird, wird die Maßzahl des Flächeninhaltes hier negativ.
Also ist $A_{D} = 124 FE .$

Vektordarstellung

Das Dreieck ABC werde durch die Vektoren $\vec{c} = \vec{A B} u n d \vec{b} = \vec{A C}$ aufgespannt:

Bild

Wegen $h = | \vec{b} | \cdot \sin α$ gilt für den Flächeninhalt des Dreiecks ABC:
$\begin{array}{l} A = \frac{1}{2} | \vec{c} | \cdot h \\ = \frac{1}{2} | \vec{b} | | \vec{c} | \cdot \sin α \end{array}$

Bei Benutzung des Vektorproduktes ergibt sich die folgende Form:
$A = \frac{1}{2} | \vec{b} \times \vec{c} |$

Beispiel 2: Gegeben sind die Punkte $A (1; 1; 1), B (2; 3; 4) u n d C (4; 3; 2)$ . Es ist der Flächeninhalt des Dreiecks ABC zu berechnen.

Es ist $\vec{b} = (\begin{matrix} 3 \\ 2 \\ 1 \end{matrix}) u n d \vec{c} = (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) .$
Damit ergibt sich:
$A_{D} = \frac{1}{2} | (\begin{matrix} 3 \\ 2 \\ 1 \end{matrix}) \times (\begin{matrix} 1 \\ 2 \\ 3 \end{matrix}) | = \frac{1}{2} | (\begin{matrix} 4 \\ - 8 \\ 4 \end{matrix}) | = 2 | (\begin{matrix} 1 \\ - 2 \\ 1 \end{matrix}) | = 2 \sqrt{6}$

Die Fläche des Dreiecks beträgt $2 \sqrt{6} FE .$

Beispiel 3: Gegeben sind die Punkte $A (2; - 1; 3), B (1; 1; 2) u n d C (0; 3; 1)$ .
Es ist der Flächeninhalt des Dreiecks ABC zu berechnen.

Mit $\vec{b} = (\begin{matrix} - 1 \\ 2 \\ - 1 \end{matrix}) u n d \vec{c} = (\begin{matrix} - 2 \\ 4 \\ - 2 \end{matrix})$
ergibt sich:
$A_{D} = \frac{1}{2} | (\begin{matrix} - 1 \\ 2 \\ - 1 \end{matrix}) \times (\begin{matrix} - 2 \\ 4 \\ - 2 \end{matrix}) | = 0$

Der Flächeninhalt besitzt die Maßzahl 0, d.h., die drei Punkte A, B und C liegen auf einer Geraden (sind kollinear).

Lernprobleme in Mathe?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Mathe durchstarten

Verwandte Artikel

Angaben zum Lexikon

Impressum

Flächeninhalt eines Dreiecks

Umfang und Flächeninhalt von Dreiecken

Koordinatendarstellung

Vektordarstellung

Rechtliches

Einloggen