Der Grenzwertsatz von Moivre-Laplace

ABRAHAM DE MOIVRE (1667 bis 1754) war ein aus Frankreich nach England vertriebener Mathematiker, der sich in London u.a. mit Ratschlägen für Glücksspieler durchs Leben schlagen musste.

In diesem Zusammenhang war er dringend an einer numerischen Approximation der Binomialverteilung interessiert, denn vor allem aufsummierte Binomialwahrscheinlichkeiten $B_{n;p}\left(\left\{0;1;\mathrm{...};k\right\}\right)$ für große n oder für „krumme“ Werte von p lassen sich schwer berechnen.

Er löste das Problem für $p=\mathrm{0,5}$, indem er die Grenzverteilung für $n\to \infty$ herleitete.
LAPLACE konnte den Nachweis über die Annäherung der Binomialverteilung an die Normalverteilung für beliebige p erbringen. Ihn interessierte dabei nicht nur die Problematik der numerischen Approximation der Binomialverteilung, sondern auch die der Anwendungsmöglichkeiten der Normalverteilung.

Der Grenzwertsatz von MOIVRE-LAPLACE besagt das Folgende:

• Ist X eine binomialverteilte Zufallsgröße mit $X\sim B_{n;p}$, dann gilt:
  $(1)\underset{n\to \infty }{\lim }{B}_{n;p}\left(\left\{k\right\}\right)=\frac{1}{\sigma }\cdot \varphi \left(\frac{k-\mu }{\sigma }\right)$ $(2)\underset{n\to \infty }{\lim }{B}_{n;p}\left(\left\{0;1;\mathrm{...};k\right\}\right)=\Phi \left(\frac{k-\mu }{\sigma }\right)$
  (wobei $\mu =EX=n\cdot p$ und $\sigma =\sqrt{D^{2}X}=\sqrt{n\cdot p\cdot \left(1-p\right)}$
  sowie $\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{1}{2}{x}^2}$ und $\Phi \left(x\right)={\displaystyle \underset{-\infty }{\overset{x}{\int }}\varphi \left(t\right)}dt$ ist)

Praktisch wird dieser Satz vor allem zum näherungsweisen Berechnen von Binomialwahrscheinlichkeiten verwendet.

Für $n\cdot p\cdot \left(1-p\right)>9$ (Faustregel) sind die folgenden Näherungsformeln sinnvoll:
$\begin{array}{l}{B}_{n;p}\left(\left\{k\right\}\right)\approx \frac{1}{\sigma }\varphi \left(\frac{k-\mu }{\sigma }\right)(lokaleNäherung)\\ B_{n;p}\left(\left\{0;1;\mathrm{...};k\right\}\right)\approx \Phi \left(\frac{k+\mathrm{0,5}-\mu }{\sigma }\right)(globaleNäherung)\end{array}$

Anmerkung: Der in der globalen Approximation enthaltene Summand 0,5 hat keinen mathematisch begründbaren Hintergrund. Sein Einfügen beruht auf Erfahrung.
Die Formel wird auch ohne den Korrektursummanden 0,5 genutzt.

Ein Anwendungsproblem und seine Lösung

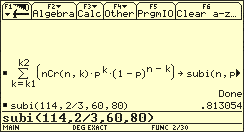
Beispiel: Am diesjährigen Schulsportfest der 11. und 12. Klassen des „Lauf-dich-gesund-Gymnasiums“ nehmen 114 Schüler teil. Die Mitarbeiterinnen der Schulkantine bieten zur besonderen Stärkung Steak vom Laufschwein an. Aus Erfahrungen vergangener Jahre wissen sie, dass im Mittel zwei Drittel der Sportfestteilnehmer von diesem Angebot Gebrauch machen. Sie bereiten deshalb 80 Portionen zu, wobei der Verkaufspreis so kalkuliert wurde, dass bei einem Verkauf von weniger als 60 Steaks ein finanzieller Verlust entsteht.
Mit welcher Wahrscheinlichkeit stärken sich zwischen 60 und 80 Sportfestteilnehmer mit einem Steak vom Laufschwein?

Modellfindung:
Wenn man davon ausgeht, dass sich die Sportfestteilnehmer unabhängig voneinander entscheiden, ob sie ein Steak kaufen oder nicht (diese Annahme wird im realen Geschehen nicht immer erfüllt sein), dann ist die zufällige Anzahl X der ess- und kaufwilligen Sportfestteilnehmer binomialverteilt mit den Parametern $n=114undp=\frac{2}{3}$.

Für die gesuchte Wahrscheinlichlichkeit gilt:
$P\left(60\le X\le 80\right)=B_{114;\frac{2}{3}}\left(\left\{0;1;\mathrm{...};80\right\}\right)-B_{114;\frac{2}{3}}\left(\left\{0;1;\mathrm{...};59\right\}\right)$

Der Faustregel wird genügt, denn es ist:
$n\cdot p\cdot \left(1-p\right)=114\cdot \frac{2}{3}\cdot \frac{1}{3}=\mathrm{25,}\overline{3}>9$

Die globale Näherung mit $\mu =EX=n\cdot p=114\cdot \frac{2}{3}=76$ und $\sigma =DX=\sqrt{n\cdot p\cdot \left(1-p\right)}=\sqrt{114\cdot \frac{2}{3}\cdot \frac{1}{3}}=\sqrt{\frac{76}{3}}=\sqrt{\mathrm{25,}\overline{3}}$ liefert:
$P\left(60\le X\le 80\right)\approx \Phi \left(\frac{80+\mathrm{0,5}-76}{\sqrt{\mathrm{25,}\overline{3}}}\right)-\Phi \left(\frac{59+\mathrm{0,5}-76}{\sqrt{\mathrm{25,}\overline{3}}}\right)$

Unter Verwendung von Tabellenwerten erhält man:
$\begin{array}{l}P\left(60\le X\le 80\right)\approx \Phi \left(\mathrm{0,89}\right)-\Phi \left(-\mathrm{3,28}\right)\\ =\Phi \left(\mathrm{0,89}\right)-\left(1-\Phi \left(\mathrm{3,28}\right)\right)\\ \approx \mathrm{0,8133}-\left(1-\mathrm{0,9995}\right)=\mathrm{0,8128}\end{array}$
Die gesuchte Wahrscheinlichkeit beträgt also näherungsweise 0,81.
Die folgende Abbildung zeigt die „exakte“ Lösung.