Differenzialgleichungen zur Beschreibung des Lade- und Entladevorgangs eines Kondensators
In einem Gleichstromkreis befindet sich eine Spannungsquelle mit der Spannung ein ohmscher Widerstand R und ein Kondensator mit der Kapazität C.
Wird Spannung angelegt, so fließt über den Widerstand R ein Strom I zum Kondensator und lädt ihn auf. Dabei wächst die Kondensatorspannung
Beim Stromfluss fällt am Widerstand die Spannung ab. Die Summe aus Spannungsabfall am ohmschen Widerstand und Kondensatorspannung ist immer gleich der Spannung der Spannungsquelle.
Es gilt also woraus mit folgt:
Diese Gleichung ist eine lineare inhomogene Differenzialgleichung 1. Ordnung der Form mit den Koeffizienten sowie der gesuchten Funktion , die im Folgenden zu lösen ist.
-
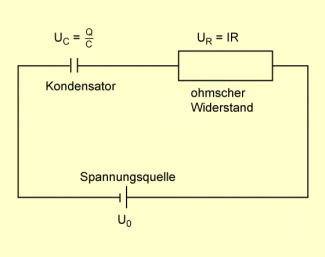
Gleichstromkreis mit Spannungsquelle, Kondensator und ohmschen Widerstand
Aus der allgemeinen Lösung
erhält man als Lösung der Gleichung:
Nun werden die Anfangswertprobleme für den Lade- und Entladevorgang des Kondensators gelöst. Beim Laden liefert die Spannungsquelle die Spannung zu Beginn des Ladevorgangs befindet sich noch keine Ladung auf dem Kondensator. Beim Entladen liegt keine äußere Spannung an, der Kondensator verfügt bei über eine Spannung und trägt demzufolge die Ladung
| Ladevorgang | Entladevorgang | |
| Bedingungen | ||
| Gleichung lösen | ||
| partikuläre Lösung für Q | ||
| Spannung am Kondensator | ||
| Spannung am Kondensator mit |
Wir betrachten nun den folgenden Spannungsverlauf für einen Lade- und einen Entladevorgang. Die Kapazität des Kondensators beträgt Die Spannungsquelle hat beim Einschalten eine Spannung von 40 V, die gleiche Spannung hat auch der Kondensator beim Abschalten. Der ohmsche Widerstand beträgt .
-
Spannungsverlauf für einen Lade- und einen Entladevorgang eines Kondensators
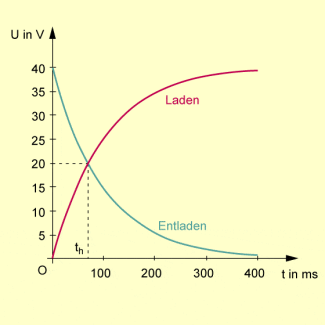
Um eine geeignete Einteilung der Zeitachse zu ermöglichen, wird zuerst diejenige Zeit ermittelt, die verstreicht, bis der Kondensator mit einer Spannung von 40 V zur Hälfte entladen ist:
Die grafische Darstellung erfolgt mit Blick auf die Halbwertszeit im Zeitintervall von 0 bis 0,4 s bzw. von 0 bis 400 ms. Ferner gilt

